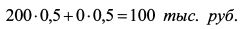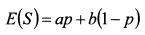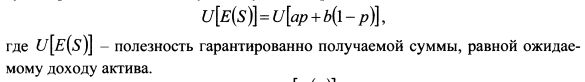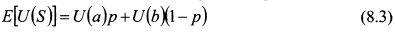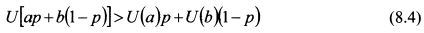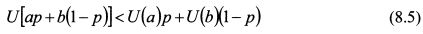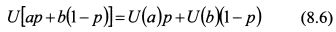|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
8.1.2. Общая характеристика функций полезности и ожидаемой полезностиВ основе концепции полезности лежит функция полезности инвестора. Она представляет собой зависимость между полезностью, получаемой инвестором от владения богатством, и уровнем этого богатства. Поскольку полезность является субъективным понятием для каждого человека, она трудно сравнима между разными лицами. Однако использование функции полезности позволяет дать характеристику действиям конкретного инвестора и, соответственно, лучше понять общий вектор принятия решений участниками рынка. Чтобы анализировать поведение инвестора с помощью функции полезности, необходимо определить ее форму. Как было отмечено в параграфе 8.1.1, разумно предположить, что инвестор всегда предпочтет большее количество богатства его меньшему количеству, поскольку больший уровень богатства открывает дополнительные возможности для реализации его потребностей. Поэтому функция полезности должна иметь возрастающую форму. Владение богатством (деньгами, активами) приносит инвестору полезность. Рост количества богатства приносит ему дополнительную, т.е. предельную полезность. С ростом богатства увеличивается общая величина полезности. Однако следует подчеркнуть, что, предельная полезность не обязательно пропорциональна количеству получаемого дополнительного богатства. Кроме того, для разных инвесторов единица богатства может обладать разной полезностью. Проиллюстрируем сказанное на примере. Пример. Инвестиции в 100 тыс. руб. с равной вероятностью могут принести доход либо в 200 тыс. руб., либо нулевой доход. Тогда ожидаемый доход от инвестиций равен:
Можно ли такой ожидаемый результат рассматривать как приемлемый для инвестора? Ответ на вопрос не в последнюю очередь зависит от его финансового положения. Если 100 тыс. руб. - это вся сумма, которой располагает инвестор, то скорее всего рассчитанный результат для него не подходит: потенциальный риск потерять всю сумму денег не компенсируется адекватным потенциальным вознаграждением - получением в случае успеха 200 тыс. руб. Напротив, если инвестор располагает большим капиталом, например, в 1 млн. руб., то риск для него может оказаться приемлемым. Таким образом, индивидуальная полезность одной и той же суммы денег (100 тыс. руб.) не одинакова для первого и второго инвесторов. Для второго лица она меньше, поэтому оно готово рискнуть, несмотря на возможность потерять деньги. Большая часть решений в экономике принимается в условиях неопределенности будущей конъюнктуры. Поэтому выбор инвестора в условиях риска основывается на функции ожидаемой полезности. Поскольку результат от владения активом точно не определен, то, принимая решение о его покупке, необходимо учитывать как возможный доход, так и риск неполучения этого дохода. В связи с этим в качестве аргументов функции ожидаемой полезности следует рассматривать ожидаемый доход (богатство) и риск неполучения данного дохода. Как было показано в приведенном выше примере, принятие инвестиционного решения зависело не только от абсолютной величины ожидаемого результата, но и его возможной дисперсии, т.е. риска неполучения положительного результата. В примере абсолютная величина дисперсии результата изменялась от полной потери инвестированных денег до получения 200 тыс. руб. Такая дисперсия была неприемлема для первого инвестора и допустима для второго. В примере ожидаемый результат - потенциальный прирост богатства - и его дисперсия были представлены в абсолютных величинах, в рублях. Картина принципиально не изменится, если от абсолютных величин перейти к относительным, т.е. представить ожидаемый результат показателем доходности инвестиций, а риск - показателем дисперсии доходности. Всех инвесторов можно разделить на три группы: а) не склонных к риску; б) склонных к риску и в) нейтральных к риску. Инвестор считается не склонным к риску, если из двух активов с одинаковой ожидаемой доходностью, но разным риском, он выберет менее рискованный актив, т.е. актив с меньшей дисперсией результатов. В финансовой теории полагается, что большинство инвесторов не склонны к риску. Это, однако, не означает, что они не готовы идти на более высокий риск. Это говорит лишь о том, что в случае увеличения риска актива в качестве потенциальной компенсации они требуют и более высокой ожидаемой доходности с его стороны. Инвестор считается склонным к риску, если из двух активов с одинаковой ожидаемой доходностью, но разным риском, он выберет более рискованный актив, т.е. актив с большей дисперсией результатов. Такой инвестор предпочитает рискнуть в надежде получить более высокую доходность в случае благоприятного исхода, однако может понести и потери при неблагоприятном развитии событий. Он рассчитывает получить дополнительную полезность от дополнительного риска. Инвестор считается нейтральным к риску, если он не учитывает его при принятии инвестиционных решений. Это означает, что инвестор безразличен в выборе между двумя активами с одинаковой ожидаемой доходностью, но разным риском. Как правило, инвесторы нейтральны к риску для его небольших значений. Как было отмечено выше, функция полезности, т.е. зависимость полезности от уровня богатства, является возрастающей. Однако ее форма должна отличаться в зависимости от степени склонности инвестора к риску. Для выяснения формы функции полезности каждой группы инвесторов, определим их несколько иначе, чем было сделано выше. Пусть инвестор может выбирать между покупкой актива и гарантированным получением суммы денег равной по величине ожидаемому доходу этого актива. В первом случае возникает риск, так как фактический доход по активу может оказаться как выше, так и ниже его ожидаемого дохода. Инвестор, предпочитающий получить сумму денег равную ожидаемому доходу актива, чем купить актив, является не склонным к риску. Инвестор, выбирающий покупку актива, вместо получения суммы денег равной его ожидаемому доходу, является склонным к риску. Инвестор безразличный в выборе между получением суммы денег равной ожидаемому доходу актива и его покупкой является нейтральным к риску. Переформулируем приведенные определения с использованием понятий функций полезности и ожидаемой полезности. Инвестор является не склонным к риску, если значение функции полезности от получаемой суммы денег равной ожидаемому доходу, больше значения функции ожидаемой полезности от покупки актива. Инвестор склонен к риску, если значение функции полезности от получаемой суммы денег равной ожидаемому доходу актива меньше значения функции ожидаемой полезности от покупки актива. Если оба значения для него одинаковы, он нейтрален к риску. Пусть некоторый актив S может принести только два результата - доход а с вероятностью р и доход b с вероятностью (l - р). Тогда ожидаемый доход актива E(s) составляет:
Величина полезности, получаемая инвестором как функция от гарантированной суммы равной ожидаемому доходу актива, равна:
Значение ожидаемой полезности E[U/(S)] рискованного актива, на которое инвестор ориентируется при принятии решения о его покупке, определяется как средневзвешенная полезность каждого из возможных фактических результатов. Весами выступают вероятности исходов. В нашем случае она равна:
Функция (8.3) является линейной комбинацией полезностей U(a) и U(b) для разных значений вероятностей исходов. Поэтому графически она представляет собой прямую линию, соединяющую эти точки. Выше мы определили, что инвестор не склонен к риску, если значение его функции полезности от суммы, соответствующей ожидаемому доходу, больше значения ожидаемой полезности от покупки актива, т.е. U[E(S)] > E[U(S)] или:
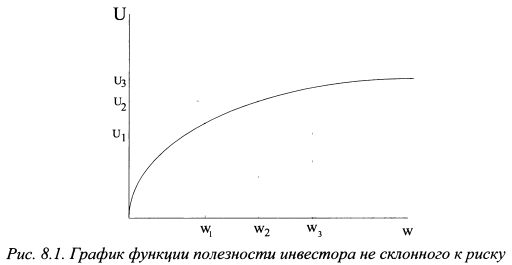
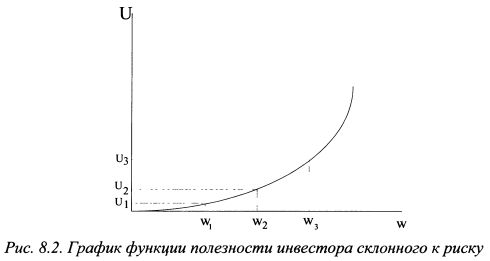
Поскольку графически правая часть неравенства (8.4) - это прямая линия, то его левая часть должна представлять собой выпуклую вверх функцию на участке аb. Таким образом, неравенство (8.4) показывает, что функция полезности инвестора не склонного к риску имеет выпуклую вверх форму. Ее график представлен на рис. 8.1. По оси ординат откладывается полезность (U), по оси абсцисс - богатство (w). Как видно из графика, по мере роста богатства инвестора растет и его общая полезность, однако дополнительная, или предельная, полезность богатства падает. Это означает, что с увеличением богатства инвестора на одинаковую величину получаемая им предельная полезность уменьшается, т.е. функция предельной полезности его богатства является убывающей. Так, при росте богатства с w1 до w2 полезность инвестора выросла с U1 до U2. При дальнейшем росте богатства на такую же величину с w2 до w3 предельная полезность выросла на меньшую величину - с и2 до и3. График также показывает, что изменение богатства на одну и ту же величину вызывает большее падение полезности инвестора при уменьшении богатства, чем при его росте. Если богатство инвестора в данный момент находится на уровне w2, то уменьшение его до величины н>, приведет к большей потери полезности, чем ее увеличение при росте богатства до w3. He склонный к риску инвестор при утрате части богатства теряет больше полезности, чем получает ее при приросте богатства на такую же величину. Поэтому среди рискованных активов с одинаковым уровнем ожидаемой доходности он всегда выберет менее рискованный. Поскольку функция полезности не склонного к риску инвестора является возрастающей, то ее первая производная положительна, т.е. U'(w)>0. Предельная полезность является величиной убывающей, поэтому вторая производная функции полезности отрицательна, т.е. U"(w)< 0.
Для инвестора склонного к риску величина полезности получаемого дохода равного ожидаемому доходу актива меньше величины ожидаемой полезности от покупки актива, т.е. U[E(S)] < E[U(S)] или:
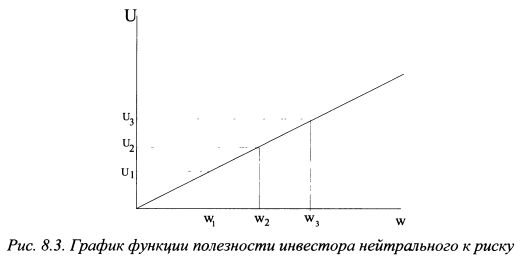
Правая часть неравенства (8.5) является прямой линией. Следовательно, его левая часть должна быть функцией выпуклой вниз на участке аb. Таким образом, неравенство (8.5) показывает, что функция полезности инвестора склонного к риску имеет выпуклую вниз форму. Она изображена на рис. 8.2.
Из графика видно, что предельная полезность богатства инвестора склонного к риску возрастает по мере роста его богатства. Кроме того, при изменении богатства на одинаковую величину при его росте его предельная полезность увеличивается в большей степени в сравнении с ее падением при уменьшении богатства. В результате, среди активов с одинаковым ожидаемым доходом, но разным риском, инвестор предпочтет более рискованный актив. Поскольку функция полезности не склонного к риску инвестора является возрастающей, то ее первая производная положительна, т.е. U'(w) > 0. Предельная полезность является величиной возрастающей, поэтому вторая производная функции полезности также положительна, т.е. U"(w) > 0. Для инвестора нейтрального к риску характерно равенство значений U[E(S)] И E[U(S)] или:
Поэтому график его функции полезности представляет собой прямую линию, как показано на рис. 8.3. Для него величина предельной полезности остается неизменной при изменении богатства. |
||||||||||||
|
|
||||||||||||