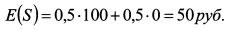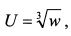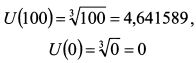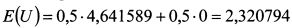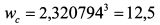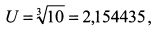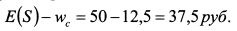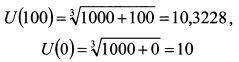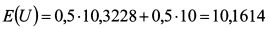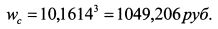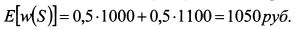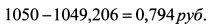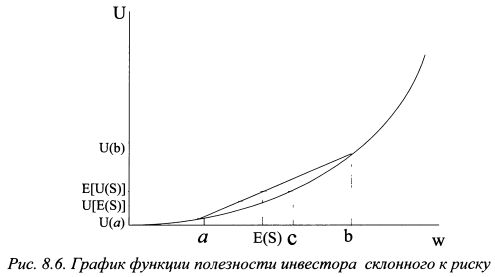
8.1.3. Премия за риск Марковца

Для инвестора не склонного к риску для каждого рискованного актива можно определить сумму денег, при которой он безразличен в выборе между ее гарантированным получением и покупкой данного актива. Эту сумму называют гарантированной эквивалентной суммой. Данный случай проиллюстрирован на рис. 8.4. На графике представлены два значения ожидаемого дохода - а и b, которые может принести рискованный актив S с вероятностями исходов - р и (l - р). Ожидаемый доход актива составляет:

Ожидаемая полезность от покупки рискованного актива равна E[U(S)]. На рис. 8.4 ее значение найдем, опустив перпендикуляр из точки е на ось ординат. Не склонный к риску инвестор не будет покупать данный актив, поскольку полезность от получения гарантированной суммы E(S) согласно графику составляет U[E(S)] и она больше величины E[U(S)]. В то же время на графике функции полезности существует точка g, соответствующая доходу с, в которой полезность инвестора такая же как и в точке е. Это говорит о том, что с точки зрения полезности инвестор безразличен в выборе между гарантированным получением суммы с и покупкой рискованного актива с ожидаемым доходом E(S). Уровень дохода с является эквивалентным гарантированным доходом, соответствующим ожидаемому доходу E(S).

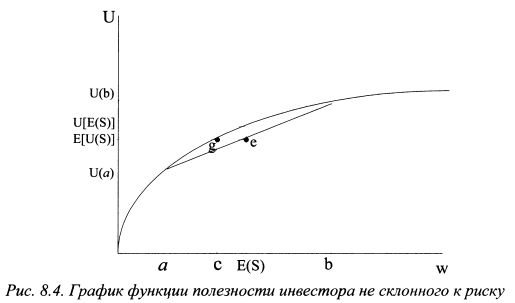
Из графика следует, что для не склонного к риску инвестора ожидаемый доход актива должен быть больше гарантированной суммы. Эту разность именуют премией за риск Марковца. На рис. 8.4 ее величина равна [E(S)-c]. Премия за риск представляет собой вознаграждение, которое делает инвестора безразличным в вопросе выбора рискованного актива с ожидаемым доходом E(S) или безрискового актива с доходом с. Премию за риск можно определить как ту максимальную сумму денег, от которой инвестор готов отказаться, чтобы исключить неопределенность результата, связанного с рискованным активом, или как ту максимальную сумму денег, которую он готов заплатить, чтобы гарантировать по рискованному активу результат равный его ожидаемому доходу. В последнем случае данную сумму удобно представить как стоимость страхового полиса, приобретаемого вместе с рискованным активом. Чем менее склонен к риску инвестор, тем больший ожидаемый доход должен предлагать актив по сравнению с эквивалентным доходом. Такая зависимость говорит о том, что чем меньше склонность к риску, тем более выпуклой должна быть функция полезности. На рис. 8.5 функция полезности более выпукла в сравнении с рис. 8.4. В результате разность [E(S)-c] также больше.

Для не склонного к риску инвестора разность [E(S)-c] является величиной положительной. На основе сказанного можно сделать вывод о том, что не склонный к риску инвестор выберет рискованный актив, если премия за риск для него больше премии за риск Марковца и актив без риска, если она меньше. При равенстве данных величин оба актива для него являются одинаковыми.

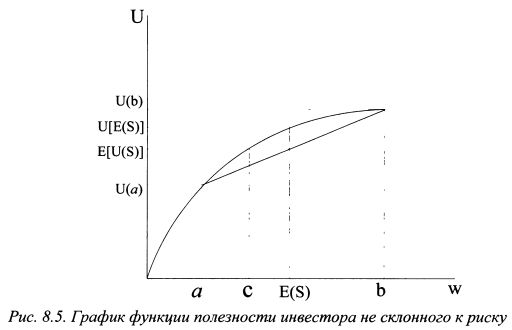
Для инвестора склонного к риску наблюдается обратная ситуация. Гарантированная эквивалентная сумма для него должна быть больше ожидаемого дохода (см. график 8.6), и разность [E(S)-c] является отрицательной величиной.

Рассмотрим на примерах, как можно определить величину гарантированной эквивалентной суммы для рискованных инвестиций и премию за риск Марковца.

Пример 1.

Инвестор участвует в лотерее S. С равной вероятностью он может ничего не выиграть или выиграть 100 руб. Определить стоимость лотереи, чтобы инвестор был безразличен в вопросе участия в ней, если его функция полезности имеет вид: .

Решение.

Ожидаемый доход в лотерее равен:

Функция полезности инвестора имеет вид:

поэтому ожидаемую полезность найдем как:

Из формулы (8.7) определим значение гарантированной эквивалентной суммы для данного уровня ожидаемой полезности рискованных инвестиций:

Полезность инвестора в случае реализации первого и второго исходов лотереи соответственно равна:

Ожидаемая полезность лотереи составляет:

На основе (8.8) гарантированная эквивалентная сумма (w_c), полезность которой равна ожидаемой полезности лотереи, составляет:

Отсюда можно сделать вывод: для лотереи с ожидаемым доходом в 50 руб. при стоимости лотерейного билета 12,5 руб. инвестор безразличен в вопросе участия или неучастия в ней. Если билет стоит меньше 12,5 руб., то инвестор будет в ней участвовать, так как ожидаемая полезность лотереи больше полезности от суммы стоимости лотерейного билета. Например, билет стоит 10 руб., тогда полезность данной суммы составляет для инвестора:

это меньше величины ожидаемой полезности от лотереи - 2,320794.

Если лотерейный билет стоит больше 12,5 руб., то инвестору следует не участвовать в лотерее, так как полезность суммы стоимости лотерейного билета больше ожидаемой полезности от лотереи.

Премия за риск Марковца равна:

Если премия за риск Марковца больше 37,5 руб., т.е. билет стоит меньше 12,5 руб., то инвестор будет участвовать в лотерее, если она меньше, он не примет в ней участия. Сумму в 37,5 руб. можно определить как ту страховку, которую готов уплатить инвестор, чтобы гарантированно получить сумму равную ожидаемому доходу лотереи, т.е. 50 руб. Данную сумму можно рассматривать как меру ценности для инвестора гарантированной суммы дохода в 50 руб.

Пример 2.

В примере 1 мы не учитывали состояние богатства инвестора. Рассчитаем премию Марковца для случая, если начальное богатство инвестора составляет 1000 руб. Из этой суммы инвестор покупает лотерейный билет.

Полезности от всего богатства инвестора в случае реализации первого и второго исходов лотереи соответственно равны:

Ожидаемая полезность богатства с учетом ожидаемых результатов лотереи составляет:

Гарантированная эквивалентная сумма, полезность которой равна ожидаемой полезности богатства с учетом возможного результата лотереи, составляет:

Величина ожидаемого богатства инвестора с учетом лотереи равна:

Отсюда премия Марковца составляет:

Таким образом, инвестор готов уплатить сумму (страховку) в 0,794 руб., чтобы гарантировать получение суммы эквивалентной ожидаемому доходу лотереи, т.е. 50 руб., чем испытывать случайный результат выиграть 100 руб. или ничего не выиграть.

Как было отмечено выше, с ростом богатства не склонного к риску инвестора его предельная полезность уменьшается. Приведенные примеры характеризуют данную ситуацию. Пример 1 можно рассматривать как случай с нулевым начальным богатством инвестора. Во втором примере начальное богатство составляло 1000 руб. В первом примере ценность гарантированной суммы равной ожидаемому доходу лотереи, т.е. 50 руб., была для инвестора выше, чем во втором. Для обеспечения ее получения он готов был уплатить страховку в 37,5 руб., а во втором примере - только 0,794 руб., т.е. ценность единицы денег для инвестора во втором случае уменьшилась. Поэтому он готов уплатить за гарантированное получение того же результата меньшую стоимость.

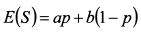
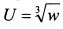Содержание

Далее