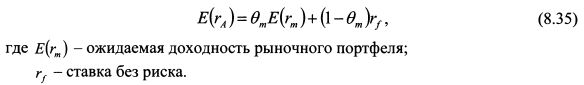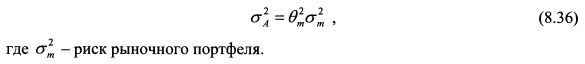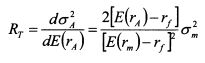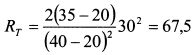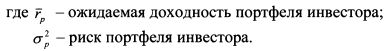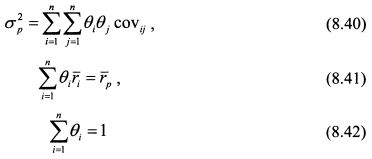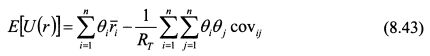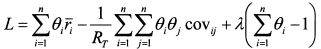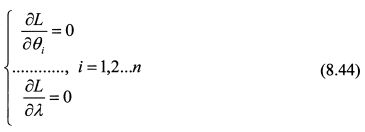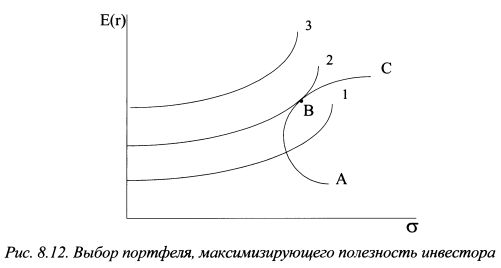
8.2. Выбор оптимального портфеля

Функцию ожидаемой полезности инвестора в виде кривых безразличия можно использовать для выбора оптимального портфеля, который бы позволил максимизировать ожидаемую доходность и минимизировать риск. Идея выбора графически представлена на рис. 8.12. Для определения оптимального портфель необходимо на на одном рисунке представить эффективную границу и кривые безразличия (см. рис. 8.12). Для примера здесь представлена эффективная граница Марковца. Вкладчик заинтересован в максимизации ожидаемой полезности, поэтому он должен ориентироваться на портфели, которые располагались бы на самой высоко расположенной кривой безразличия. Однако потенциальный выбор портфелей ограничен эффективной границей ABC. Поэтому портфель, обладающий для вкладчика наибольшей полезностью, будет находиться в точке касания эффективной границы и кривой безразличия 2 (портфель В), так как это самая высокая из доступных для инвестора кривых безразличия. В этой точке угол наклона эффективной границы равен тангенсу угла наклона кривой безразличия.

Для нахождения оптимального портфеля инвестора менеджеру необходимо определить значение его коэффициента R_T. Это можно сделать следующим образом. Менеджер строит эффективную границу на основе ставки без риска и рыночного портфеля. После этого клиенту предлагается выбрать на эффективной границе портфель, который бы в большей степени соответствовал его представлениям о риске и доходности. Допустим, он выбирает портфель А. Это означает, что угол наклона кривой безразличия в этой точке равен тангенсу угла наклона эффективной границы.

Пусть уд. вес в портфеле А рыночного портфеля равен 9т. Тогда уд. вес актива без риска равен 1 — вт. Ожидаемая доходность портфеля А составляет:

Риск портфеля А пропорционален риску рыночного портфеля и равен:

Из уравнения (8.35) уд. вес рыночного портфеля можно представить как:

Подставим значение вт из уравнения (8.37) в уравнение (8.36):

Продифференцировав уравнение (8.38) по Е(гА), получим значение коэффициента допустимости риска:

Пример.

Ставка без риска равна 20%, ожидаемая доходность рыночного портфеля -40%, портфеля из безрискового актива и рыночного портфеля - 35%, риск рыночного портфеля - 30%. Определить коэффициент допустимости риска.

Решение.

Он равен:

Задача менеджера состоит в том, чтобы определить наиболее высоко расположенную кривую безразличия, доступную инвестору. Для этого достаточно определить значение E\U(r)], принадлежащее кривой безразличия, которая является касательной к эффективной границе. Доходность в точке ?[?/(г)] называют гарантированной эквивалентной доходностью, так как с точки зрения полезности она эквивалентна доходности портфеля в точке касания кривой безразличия эффективной границы, ^[[/(г)] определяется из уравнения (8.34):

Допустим, менеджер должен максимизировать значение 2s[t/(r)J в уравнении (8.39). Ему необходимо определить, какое количество различных активов следует включить в портфель при известном значении RT. Задача для случая возможности отрицательности уд. весов активов в портфеле решается с помощью метода множителей Лагранжа. Ее можно сформулировать следующим образом. Максимизировать значение функции (8.39) при условии, что:

Подставим в формулу (8.39) риск портфеля из формулы (8.40) и ожидаемую доходность из формулы (8.41):

Уравнение (8.43) является целевой функцией. Составим на его основе с учетом ограничения (8.42) функцию Лагранжа:

Найдем частные производные функции L по 91, и X и приравняем их к нулю:

Решаем систему уравнений (8.44).

Найти уд. веса активов в портфеля, максимизируя значение функции (8.43), можно с помощью программы Excel.

Содержание

Далее