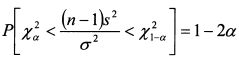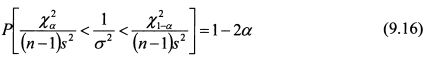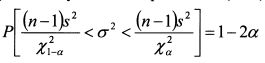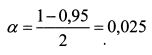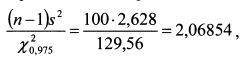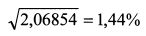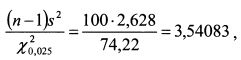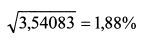|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
9.2. Оценка ошибки параметрической модели VaRVaR портфеля рассчитывается на основе выборочных данных за определенный период времени. В результате возникает необходимость оценить доверительный интервал для полученного значения VaR. По данным статистики мы определяем не истинное, а "исправленное" стандартное отклонение. В связи с этим, прежде всего, следует найти доверительный интервал для стандартного отклонения доходности портфеля. Истинное значение математического ожидания генеральной совокупности, из которой осуществляется выборка данных, также неизвестно. Поэтому для оценки доверительного интервала следует воспользоваться правилами математической статистики для случая "исправленной" дисперсии с неизвестным математическим ожиданием. Мы предполагаем, что доходность портфеля имеет нормальное распределение. Наилучшей оценкой дисперсии нормального распределения является "исправленная" дисперсия:
Разделим обе части равенства (9.12) на истинную дисперсию случайной величины (a²):
Величина
Выражение (9.14) показывает, что величина
Значения конечных точек доверительного интервала обычно выбирают таким образом, чтобы вероятности событий x² < x1² и x² > x2² были одинаковыми. Пусть эта вероятность равна а. Тогда выражение (9.15) примет вид:
или
Разделим единицу на каждую часть неравенства (9.16):
По таблице квантилей распределения х² находим нижнюю и верхнюю границы доверительного интервала дисперсии случайной величины. Квадратные корни из данных значений представляют собой нижнюю \ан) и верхнюю \сгв) границы доверительного интервала стандартного отклонения. Если в качестве случайной величины выступает доходность портфеля, то найденные значения сигм показывают доверительные границы стандартного отклонения доходности портфеля. На основе полученных данных рассчитаем доверительный интервал для VaR портфеля по формулам:
Пример. В примере 2 параграфа 9.1 мы получили однодневный VaR портфеля из двух акций в 267,3 тыс. руб. Пусть данный результат был получен на основе данных по доходности акций за 101 день. Требуется определить доверительный интервал для VaR с коэффициентом доверия у = 0,95. Решение. Из соотношения у = 1 - 2а находим значение а, соответствующее доверительной вероятности 95%:
Количество наблюдений случайной величины составило 101 день. Поэтому количество степеней свободы в примере равно 100. По таблице квантилей распределения х² находим квантили x1-a² и xa² со степенями свободы 100: x0,975²=129,56; x0,025²=74,22. Нижняя граница доверительного интервала для дисперсии равна:
а стандартного отклонения
Верхняя граница доверительного интервала для дисперсии равна:
а стандартного отклонения
По формулам (9.17) и (9.18) находим нижнюю и верхнюю границы доверительного интервала для VaR портфеля:
Таким образом, с доверительной вероятностью 95% процентов можно быть уверенным, что действительное значение VaR лежит в границах от 237,6 тыс. руб. до 310,2 тыс. руб.
|
||||||||||||
|
|
||||||||||||









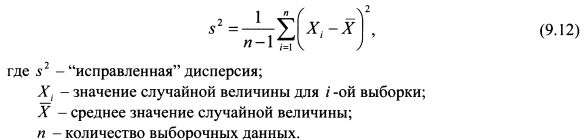
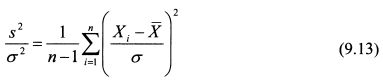
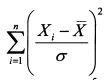 имеет распределение хи-квадрат (x²) с n-1 степенями свободы. Умножим обе части равенства (9.13) на (n-1):
имеет распределение хи-квадрат (x²) с n-1 степенями свободы. Умножим обе части равенства (9.13) на (n-1):
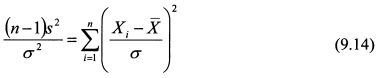
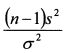 имеет х² распределение с n-1 степенями свободы. Необходимо найти границы интервала, который бы с вероятностью у накрывал истинное значение дисперсии случайной величины. Это условие записывают как:
имеет х² распределение с n-1 степенями свободы. Необходимо найти границы интервала, который бы с вероятностью у накрывал истинное значение дисперсии случайной величины. Это условие записывают как: