Приложение 2. Оценка VaR опционов с помощью дельты и гаммы

VaR опционных позиций можно оценить как на основе аналитических методов, так и с помощью метода Монте-Карло. Результаты по опционной позиции характеризуются не линейной структурой. Поэтому в большей степени для их оценки подходит метод статистических испытаний. В случае аналитического подхода опционную позицию следует разложить на ряд составляющих в соответствии с факторами риска опциона. Зависимость между премией опциона и факторами риска предполагается линейной. На практике она не линейна. Поэтому оценка VaR аналитическим способом дает приемлемый результат только для изменения факторов риска в небольшом диапазоне. Рассмотрим линейное приближение оценки VaR опциона.

Основополагающим фактором риска опциона выступает цена базисного актива. Зависимость между премией опциона и ценой базисного актива представлена дельтой опциона. Поэтому зависимость между ценой опциона в начальный и конечный моменты времени можно представить как:

На основе формулы (П.9.3) можно записать равенство:

Изменение цены базисного актива можно представить как произведение стандартного отклонения его доходности (<т) на цену, т.е.:

Тогда равенство (П.9.4) запишется как:

VaR базисного актива определяется стандартным отклонением его доходности. Поэтому для линейной зависимости при использовании допущения нормальности распределения доходности базисного актива из равенства (П.9.5) следует, что:

Недостаток равенства (П.9.3) состоит в том, что цена опциона в начале и конце периода связана линейной зависимостью. На практике она не линейна. Ошибка оценки тем больше, чем больше изменение цены базисного актива в модели. Кроме того, позиции покупателя и продавца опциона не симметричны. Уравнение не учитывает ограниченный риск покупателя и неограниченный риск продавца опциона. Дельта-оценка переоценивает риск покупателя опциона и недооценивает риск продавца опциона. Поясним это на примере опциона колл. При падении цены базисного актива дельта опциона уменьшается с ускорением. Это означает, что покупатель опциона теряет деньги с замедляющимся темпом. Однако уравнение (П.9.3) не учитывает уменьшение значения дельты. При росте цены базисного актива дельта опциона возрастает с ускорением. Поэтому продавец опциона теряет средства в возрастающем темпе. Выражение (П.9.3) в силу его линейности также игнорирует данный факт.

Важно: актуальная возможность выиграть $40–$250 реальных (не бонусных) средств в конкурсе на демо-счетах.

Поскольку дельта изменяется с изменением курса базисного актива, то лучшее приближение изменения стоимости опционной позиции можно получить на основе дельта-гамма оценки, дополнив равенство (П.9.3) гаммой опциона:

В то же время следует иметь в виду, что использование гаммы может в ряде случаев ухудшить оценку VaR. В Рискметриках банка J.P.Morgan в этой связи приводятся следующие рассуждения. Запишем равенство (П.9.7) как:

Умножим и разделим первое слагаемое в правой части равенства (П.9.8) на S, а второе слагаемое - на S²:

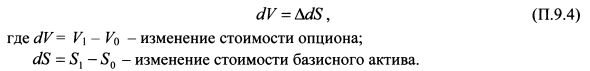
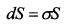
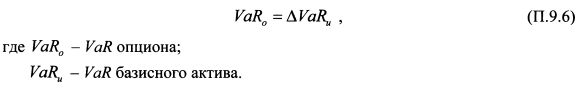
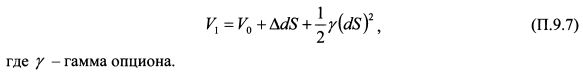
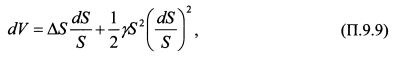
Величина 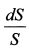представляет собой доходность базисного актива. Формула (П.9.9) говорит о том, что изменение цены опциона определяется двумя переменными - доходностью базисного актива 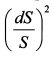и квадратом доходности . Первая случайная величина распределена нормально, вторая - по закону хи-квадрат, т.е. посылка нормальности распределения, используемая в аналитической модели нарушается. Если гамма опциона имеет большое значение - опцион ATM или до истечения которого осталось мало времени, - то это может исказить оценку за счет значительного влияния распределения хи-квадрат. При изменении цены базисного актива гамма также изменяется, поэтому дельта-гамма оценка будет содержать ошибку для существенных движений курса.

Содержание

Далее