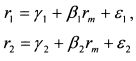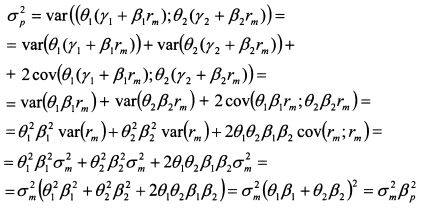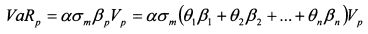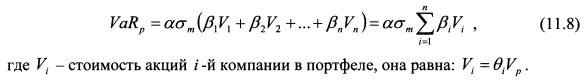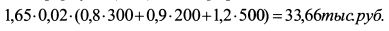|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
11.1. АкцииВ качестве стандартного актива или фактора риска для акции выступает фондовый индекс. Доходность акции связана с доходностью индекса с помощью коэффициента бета. Данная взаимосвязь представлена уравнением рыночной модели Шарпа:
Как было определено в главе 3, на основе уравнения (11.1) дисперсия и стандартное отклонение акции соответственно равны:
Если стоимость данных акций в портфеле равна Va, то VaR позиции по акции составит:
Уравнения (11.2) и (11.3) позволяют представить риск акции через риск рыночного портфеля. Риск акции содержит рыночный С учетом сказанного получим формулу риска для широко диверсифицированного портфеля. Для простоты проведем рассуждения для портфеля из двух акций. Бета первой акции /?,, второй - j32, их уд. веса в портфеле соответственно составляют 6Х и 02. Доходности акций на основе уравнения (11.1) равны:
Поскольку мы рассматриваем ситуацию для широко диверсифицированного портфеля, то специфическими рисками бумаг можно пренебречь и работать с уравнениями вида:
На основе уравнений (11.5) и (11.6) риск портфеля равен:
Таким образом, риск портфеля равен риску рыночного портфеля, умноженному на бету портфеля. В свою очередь, как следует из приведенных преобразований, бета портфеля равна средневзвешенному значению коэффициентов бет акций, входящих в портфель. В результате можно записать:
Формулу (11.7) можно также представить как:
или
Широко диверсифицированный портфель будет состоять из акций компаний разных отраслей. Тогда портфель из стандартных активов может точнее копировать риск исходного портфеля, если для проецирования рисков индивидуальных акций использовать не рыночный индекс, а отраслевые индексы для акций каждой отрасли. В таком случае в качестве стандартных активов выступают отраслевые индексы, для которых известны стандартные отклонения и ковариации с другими стандартными активами. Пример. Портфель состоит из акций трех компаний, Д = 0,8; /32 = 0,9 ; /Зъ = 1,2 . Стоимость акций первой компании в портфеле равна 300 тыс. руб., второй - 200 тыс. руб., третьей - 500 тыс. руб., стандартное отклонение рыночного портфеля для одного дня составляет 2%. Определить однодневный VaR портфеля для доверительной вероятности 95%. Решение. На основании формулы (11.8) VaR портфеля составляет:
Формулы (11.7) и (11.8) позволяют найти VaR широко диверсифицированного портфеля. Поэтому возникает вопрос о том, какой портфель можно считать таковым. Как отмечалось в главе 3, в современных условиях с полным основанием таким портфелем можно считать портфель, включающий не менее 50 акций.
|
||||||||||||
|
|
||||||||||||










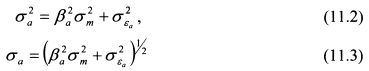
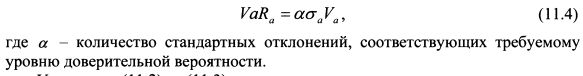
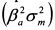 и специфический
и специфический 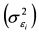 компоненты. Однако для широко диверсифицированных портфелей нерыночный риск практически равен нулю. Поэтому риск портфеля определяется только на основе рыночных рисков каждой акции, т.е. слагаемого
компоненты. Однако для широко диверсифицированных портфелей нерыночный риск практически равен нулю. Поэтому риск портфеля определяется только на основе рыночных рисков каждой акции, т.е. слагаемого 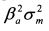 или
или 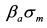 .
.