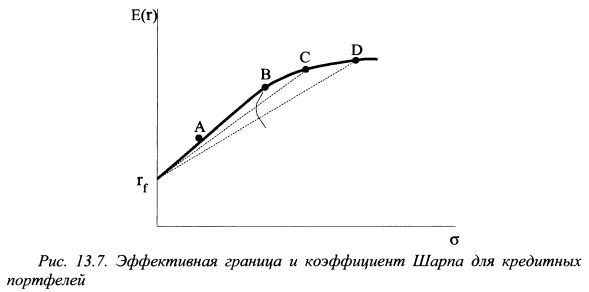
13.2.3. Недостатки индексов Шарпа, Трейнора и Дженсена

Оценка эффективности управления портфелем с помощью индекса Шарпа в теории предполагает наличие СML, которая проходит через рыночный портфель и представляет собой прямую линию. Предположим, однако, что инвесторы не имеют возможности формировать заемные портфели, но могут предоставлять деньги в кредит. Тогда эффективная граница примет форму как показано на рис. 13.7.

Пусть сравниваемые портфели А, В, С и D расположились точно на эффективной границе f/BD. Поэтому их менеджеры характеризуются одинаковым уровнем мастерства. В то же время оценка на основе коэффициента Шарпа покажет, что наиболее успешными были менеджеры портфелей А и В. Для них коэффициент Шарпа оказался одинаковым. Наименьшим коэффициентом характеризуется менеджер портфеля D. Такой результат получился потому, что, как следует из рис. 13.2, коэффициент Шарпа измеряется угловым коэффициентом наклона линии, соединяющей ставку без риска с оцениваемым портфелем. Поскольку на рис. 13.7 портфели А и В расположены на линии rfB, то угловой коэффициент наклона для них одинаков.

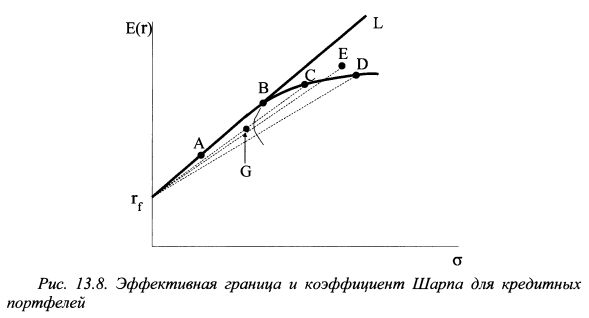
Одновременно угловой коэффициент наклона линии rfD является наименьшим. Таким образом, в отмеченной ситуации индекс Шарпа имеет тенденцию занижать результативность управления портфелями, расположенными левее точки В, т.е. точки касания линии, проведенной от ставки без риска к эффективной границе Марковца. Кроме того, из рис. 13.8 следует, что индекс Шарпа даст более низкую оценку и любому действительно эффективно управлявшемуся портфелю, если только он не расположен выше линии rfBL (она является касательной к эффективной границе). Так, например, из всех портфелей на рис. 13.8, наиболее эффективно управляемым оказался портфель Е. Однако коэффициент Шарпа покажет, что он управлялся хуже портфелей А, В и С. Соответственно портфель G также окажется лучше портфеля Е.

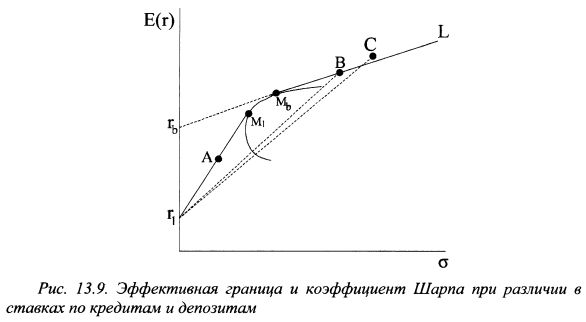
Аналогичные проблемы возникают и в ситуации, когда ставки по кредитам и депозитам не равны (см. рис. 13.9). На рис. 13.9 эффективная граница представлена линией rlMlMbL. По той же причине что и в рассмотренном выше случае коэффициент Шарпа дает заниженную оценку управляющему портфелем В по сравнению с управляющим портфелем А, хотя их уровень мастерства на самом деле одинаков. Соответственно портфель С, наиболее эффективно управлявшийся в нашей ситуации, окажется хуже портфелей и А и В, так как угол наклона пунктирной линии riC меньше углов наклона линий riA и riB. Подобные недостатки характеризуют и индекс Трейнора.

Индекс Шарпа также может дать не верную оценку при сравнении портфелей, если премия за риск портфелей оказывается отрицательной.

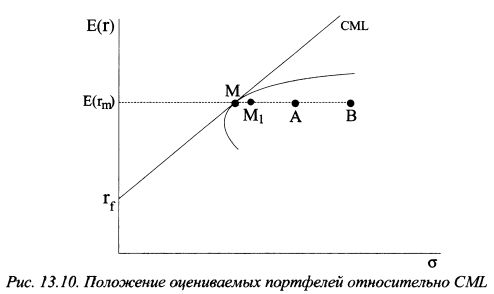
Индекс Дженсена также может исказить действительную картину эффективности управления портфелем. Для получения "верной" оценки с помощью индекса Дженсена необходимо построить SML на основе "настоящего" рыночного портфеля. Однако такой портфель существует только в теории, на практике используют приближение к нему. "Фактический" рыночный портфель может быть как угодно близок к теоретическому, но будет отличаться от него. Коэффициенты бета рассчитываются относительно "фактического" рыночного портфеля. Поэтому в зависимости от того, насколько верно был выбран "фактический" рыночный портфель, будут получены и соответствующие коэффициенты бета активов. Как отмечает Р.Ролл, "...для каждого актива можно найти индекс, чтобы получить бету любой желаемой величины...; ...если мы выберем неэффективный индекс, мы дадим заниженную оценку одним лицам с отличными способностями и завышенную оценку другим лицам с более низкими способностями." Таким образом, для разных возможных "фактических" рыночных портфелей результаты их управления одними и теми же портфелями будут различны. Сказанное можно проиллюстрировать графически. На рис. 13.10 представлены рыночный портфель М и два оцениваемых портфеля А и В. Все они имеют одинаковую доходность, но разный уровень общего риска. Так как ожидаемые доходности портфелей одинаковы, то на рис. 13.11 все они должны располагаться в одной точке М. Если фактические доходности оказались равными их ожидаемым значениям, то оба портфеля управлялись с одинаковым уровнем эффективности, так как их альфа оказалась равной нулю. Допустим теперь, что в качестве рыночного портфеля в силу неверных оценок был выбран портфель М\ (см. рис. 13.10), который не является эффективным, так как не расположен на эффективной границе. В результате относительно "неверной" SML портфели расположились как показано на рис. 13.12. Такие позиции они заняли в связи с тем, что, рассчитанные относительно портфеля М\9 их беты оказались иными, чем в ситуации на рис. 13.11. Если фактическая доходность портфелей оказалась равной ожидаемой, то, согласно рис. 13.12, портфель А управлялся более эффективно, так как его альфа положительна, а портфель В менее эффективно, поскольку его альфа отрицательна. Однако данные результаты объясняются не большим мастерством менеджера первого портфеля, а неправильно выбранным рыночным портфелем, что привело к неверной оценке их риска.

Представленные выше аргументы применимы и к характеристике индекса Трейнора. Если выбрать не эффективный индекс в качестве рыночного портфеля, то неправильно будут определены и беты портфелей. В результате индекс Трейнора даст не точную оценку.

Содержание

Далее