|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
13.3.2. Коэффициент информацииМенеджер, осуществляющий активное управление портфелем, стремится получить сверхдоходность за счет выбора отдельных активов и времени совершения сделок. Результаты деятельности получают оценку в показателе альфа портфеля, который в этом случае, как правило, отличается от нуля. Альфа портфеля рассчитывается относительно базисного индекса, используемого в качестве точки отсчета для определения результативности активной стратегии. Например, таким индексом для широко диверсифицированного портфеля может служить индекс S&P500. Менеджер стремится получить более высокую доходность в сравнении с доходностью пассивного портфеля, копирующего индекс, за счет выбора недооцененных или переоцененных на его взгляд бумаг, определения времени их покупок или продаж и варьирования удельными весами активов в портфеле по сравнению с их весами в индексе. Действия менеджера связаны с дополнительным риском, поскольку в этом случае увеличивается специфический риск портфеля. Он представляет собой отклонение фактической доходности портфеля от доходности базисного индекса, т.е. возникает ошибка слежения или остаточный риск. Ошибка слежения представляет собой не что иное как стандартное отклонение альфы портфеля менеджера. Поэтому на основе альфы портфеля и^ ошибки слежения определяется еще один коэффициент, позволяющий прогнозировать устойчивость результатов активно управляемого портфеля. Его именуют коэффициентом информации (information ratio). Данный показатель был предложен Дж.Трейнором и Ф.Блэком. Он определяется как отношение альфы портфеля к ошибке слежения:
Таким образом, коэффициент информации - это отношение сверхдоходности, получаемой менеджером, к стандартному отклонению этой сверхдоходности. Он показывает, сколько единиц сверх доходности приходится на дополнительную единицу риска портфеля. Значение коэффициента дает представление об устойчивости результата, получаемого менеджером. Чем меньше величина ошибки слежения, тем устойчивее результат от положительной альфы портфеля. Небольшая ошибка слежения говорит о том, что существует большая вероятность получить доходность близкую по значению к альфе портфеля. Другими словами, коэффициент информации определяет степень уверенности в получении положительного результата. Фактически он позволяет судить о том, насколько менеджер лучше информирован о будущей результативности работы компаний, включенных в портфель, по сравнению с другими участниками рынка. Поэтому он проводит в отношении данных бумаг активные стратегии с целью получить более высокую доходность по сравнению с эталонным рыночным индексом. Чем больше значение коэффициента, тем выше мастерство менеджера в вопросе выбора активов и времени осуществления сделок. Значение коэффициента информации на уровне 0,5 можно рассматривать как хорошее, 0,75 - как очень хорошее, а 1 - как отличное. Для расчета коэффициента следует взять статистические данные за относительно длительный период, чтобы снизить значения случайных событий на оценку результативности менеджера. Большее количество наблюдений даст более надежный результат. Целесообразно использовать помесячные данные как минимум за трехлетний период. Альфа портфеля определяется как средняя величина полученных отклонений доходности портфеля от доходности базисного индекса, т.е. она представляет собой среднюю сверхдоходность портфеля. На основе данных отклонений определяется их стандартное отклонение, которое является ошибкой слежения. Пример. Среднегодовое значение альфы составляет 2%, ошибки слежения - 2%. Коэффициент информации равен:
Как можно интерпретировать полученный результат? Альфа портфеля - это средняя сверхдоходность портфеля. Ошибка слежения - это стандартное отклонение возможного фактического результата от среднего значения сверхдоходности. Допустим, доходность и, следовательно, сверхдоходность распределены нормально. Тогда не трудно дать вероятностную оценку мастерству менеджера. На основе правила трех сигм можно сделать вывод о том, что с вероятностью 68,3% доходность портфеля менеджера в следующем периоде будет располагаться в интервале одного стандартного отклонения от значения сверхдоходности. В нашем примере это диапазон от нуля до четырех процентов. С физической точки зрения данный результат можно представить еще следующим образом. Если оценка коэффициента информации получена на основе помесячных наблюдений за период 100 месяцев (т.е. 8,3 года), то при многократном повторении наблюдений за такой же период времени менеджер в среднем будет получать доходность портфеля, которая располагается от средней сверхдоходности в диапазоне от нуля до 4% в каждых 68 месяцах из 100. При оценке мастерства разных менеджеров на основе коэффициентов информации их необходимо рассчитывать для одинаковых временных периодов с одинаковой частотой наблюдений. Более диверсифицированный портфель должен характеризоваться и более высокой величиной коэффициента, так как ошибки слежения будут в большей степени погашать друг друга вследствие эффекта диверсификации. Широко диверсифицированный портфель характеризуется только рыночным риском. Не рыночный риск для него отсутствует. Поскольку коэффициент информации учитывает только не рыночный риск портфеля, то он не подходит для сравнительной оценки между собой широко и слабо диверсифицированных портфелей. Данные для расчета коэффициента информации можно определить и на основе регрессионного анализа. Если уравнение регрессии доходности портфеля на доходность базисного индекса записать как:
Коэффициент информации рассчитывается на основе прошлых данных статистики. Однако прошлое вряд ли в точности повторится в будущем. Поэтому интересно определить продолжительность времени, в течение которого менеджеру следует управлять портфелем, чтобы с заданной вероятностью получить результат, соответствующий рассчитанному коэффициенту информации. Данный вопрос можно решить следующим образом. Формула (13.25) фактически показывает, какое количество стандартных отклонений сверхдоходности укладывается в интервале доходности от нуля до значения альфы. Поэтому запишем:
Как известно, доходность возрастает пропорционально рассматриваемому периоду времени, а риск - пропорционально квадратному корню из этого периода. Поэтому количество стандартных отклонений за время Т в формуле (13.26) составит:
или
или
Как видно из формулы (13.27), количество стандартных отклонений, укладывающихся в диапазон альфы портфеля при постоянном значении коэффициента информации пропорционально корню квадратному из времени, в течение которого управляется портфель. Поэтому, если в будущем портфель будет управляться Т лет, то при мастерстве менеджера, соответствующего коэффициенту информации IR, мы должны получить количество стандартных отклонений согласно формуле (13.27). В то же время, поскольку распределение доходности портфеля предполагается нормальным, то формула (13.27) позволяет охарактеризовать полученный результат с вероятностной точки зрения. Другими словами, если за период времени Т сверхдоходность портфеля попадает в интервал от нуля до среднего значения альфы, соответствующий Z стандартным отклонениям сверхдоходности, то в рамках нормального распределения такой результат соответствует определенной доверительной вероятности. Так, например, доверительной вероятности в 90%, считая от нуля как среднего значения и выше, соответствует интервал в 1,645 стандартных отклонений, доверительно вероятности в 95% - интервал в 1,96 стандартных отклонений. Выразим из формулы (13.27) величину Т:
Формула (13.28) позволяет ответить на вопрос, какое количество лет следует менеджеру управлять портфелем, чтобы с заданной доверительной вероятностью получить сверхдоходность портфеля, соответствующую его коэффициенту информации. Пример. Коэффициент информации менеджера равен 0,75. Определить, какое количество лет необходимо управлять портфелем, чтобы получить результат, соответствующий определенному мастерству менеджера с доверительной вероятностью 95%. Решение. Доверительной вероятности 95% соответствует 1,96 стандартных отклонений. Чтобы получить требуемый результат с заданной вероятностью необходимо управлять портфелем:
В заключение данного параграфа следует отметить, что, согласно У.Шарпу, коэффициент информации можно понимать как более общий случай коэффициента Шарпа, в котором вместо доходности без риска используется доходность рыночного индекса:
В формуле (13.29) Тт - это средняя доходность рыночного индекса, с которым сравнивается оцениваемый портфель, а величина Поскольку коэффициент информации по своей структуре аналогичен коэффициенту Шарпа, то он также как и коэффициент Шарпа может дать неверную сравнительную оценку для портфелей, которые показали отрицательную доходность сравнительно с эталонным рыночным индексом.
|
||||||||||||
|
|
||||||||||||









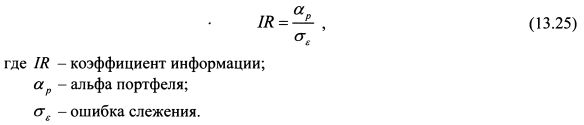
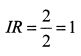
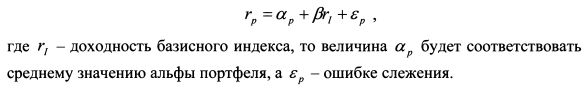
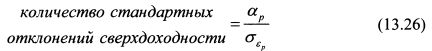
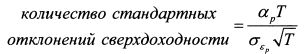
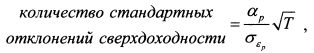
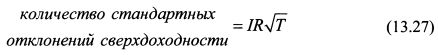



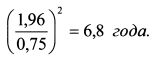

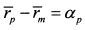 соответствует коэффициенту Дженсена портфеля.
соответствует коэффициенту Дженсена портфеля.