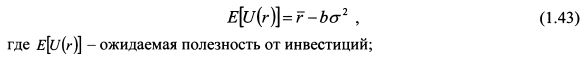|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
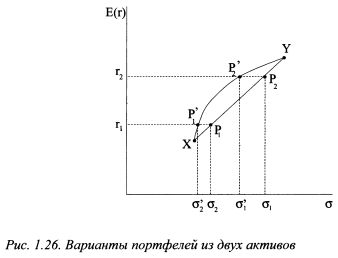
1.2.9. Эффективный набор портфелейРассмотрим портфель, состоящий из двух активов. Корреляция между доходностями активов может изменяться от -1 до +1. На рис. 1.21 все возможные комбинации портфелей, состоящих из двух бумаг с корреляцией -1, располагаются на прямых ZY и ZX. Все комбинации портфелей для корреляции +1 - на прямой XY. Комбинации портфелей для других значений корреляции доходностей располагаются внутри треугольника XZY. Таким образом, пространство треугольника XZY представляет собой все возможное множество портфелей, состоящих из двух бумаг, в пределах корреляции доходности активов от -1 до +1.
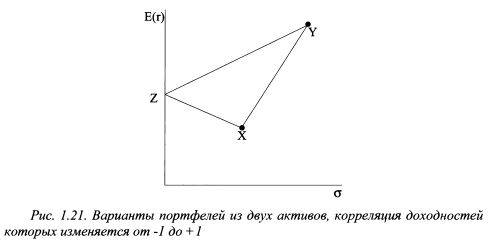
На практике подавляющая часть активов имеет корреляцию отличную от -1 и +1, и большинство активов имеют положительную корреляцию. Если построить график, на котором бы располагались портфели, состоящие из бумаг Х и F, при меньшей корреляции, чем +1, он примет выпуклый вид, как показано на рис. 1.22 сплошной линией.
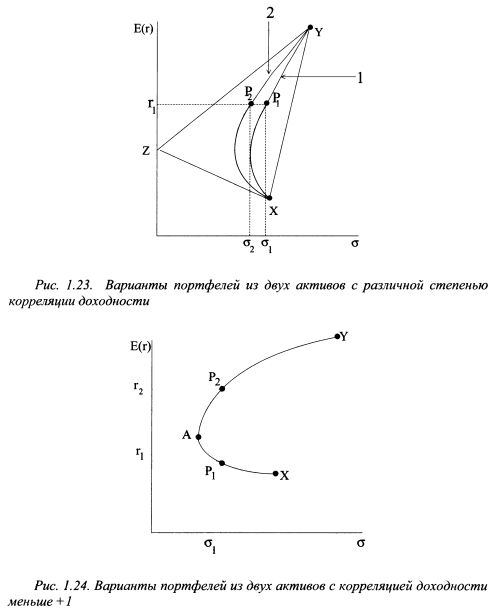
Чем меньше корреляция между доходностями активов, тем более выпуклой будет график. На рис. 1.23 линия 2 представляет меньшую корреляцию доходностей активов Х и Y по сравнению с линией 1. Как видно из рисунка, чем меньше корреляция доходностей активов, тем более они привлекательны для формирования портфеля, поскольку инвестор может получить тот же уровень ожидаемой доходности при меньшем уровне риска. Так, портфель Р2 на рис. 1.23 имеет то же значение ожидаемой доходности r1, что и портфель Рх, однако его риск меньше и равен <г2, в то время как первого портфеля – сr1. Как показано на рис. 1.24, если активы имеют корреляцию меньше +1, инвестор может сформировать любой портфель, который бы располагался на кривой XAY. Однако рациональный инвестор остановит свой выбор только на верхней части данной кривой, а именно, отрезке A F, поскольку на нем расположены доминирующие портфели. Они характеризуются более высоким уровнем ожидаемой доходности при том же уровне риска по сравнению с портфелями на участке АХ. Сравним для наглядности портфели Рх к Р2. Оба портфеля имеют риск равный <т,, но ожидаемая доходность портфеля Р2 больше ожидаемой доходности портфеля Рх. Поэтому инвестор предпочтет остановить выбор на портфеле Р2.
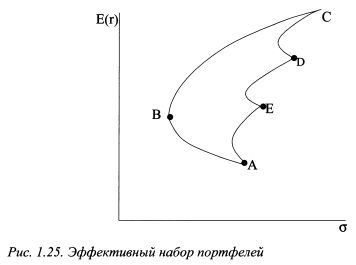
Если инвестор формирует портфель из двух бумаг, X и Y, как показано на рис. 1.24, в точке А он может получить для сочетания данных активов портфель с наименьшим уровнем риска. Его именуют глобальным портфелем. Чтобы построить такой портфель, необходимо найти удельные веса в портфеле бумаг X и F. Это можно сделать, продифференцировав уравнения (1.20) или (1.22) по вх и приравняв их к нулю при условии, что вх =\-ву. Вопрос определения уд. Весов такого портфеля был рассмотрен в параграфе 1.2.5.4. Если объединить в портфель некоторое число активов: А, Е, D и С, корреляция доходностей которых лежит в промежутке от -1 до +1, то, в зависимости от их удельных весов, можно построить множество портфелей с различными параметрами риска и доходности, которые расположены в рамках фигуры ABCDE, как показано на рис. 1.25. Рациональный инвестор будет стремиться минимизировать риск и увеличить доходность, поэтому всем возможным портфелям, представленным на рис. 1.25, вкладчик предпочтет только те, которые расположены на отрезке ВС, поскольку они являются доминирующими по отношению к портфелям с тем же уровнем риска или с той же доходностью. Набор портфелей на отрезке ВС называют эффективным набором. Эффективный набор портфелей - это набор, состоящий из доминирующих портфелей. Набор портфелей на участке ВС называют еще эффективной границей или эффективной границей Марковца. Она была открыта Г. Марковцем в 50-х годах. Чтобы определить данную границу, необходимо на основе уравнения:
рассчитать удельные веса активов в портфеле, при которых минимизируется значение его дисперсии для каждого данного уровня доходности при условии, что
Неудобство метода Марковца состоит в том, что для определения эффективной границы портфелей, включающих много активов, необходимо произвести большое количество вычислений. Если портфель состоит из n активов, то следует определить n ожидаемых доходностей и стандартных отклонений и Подход Г.Марковца к выбору эффективных портфелей называют средне-дисперсионным анализом, поскольку их построение основано на учете ожидаемой, т.е. средней доходности портфелей, и их дисперсий (стандартных отклонений). Так, на рис. 1.25 кривая ЛВС представляет собой кривую ожидаемых доходностей портфелей (в том числе отрезок ВС - эффективных портфелей). Возможные фактические результаты доходности портфелей - не равные ожидаемой - воспринимаются как отклонения от средней доходности. Таким образом, в рамках теории Г.Марковца инвесторы принимают решения на основе оценок ожидаемой доходности и дисперсии активов. Чтобы подход Г.Марковца имел практическую значимость, необходимо выполнение на практике, по крайней мере, одного из следующих двух условий, а) Доходность портфелей ценных бумаг распределена нормально. Нормальное распределение полностью определяется его математическим ожиданием и дисперсией и симметрично относительно математического ожидания. Поэтому на основе этих параметров удобно делать сравнения и выбирать между разными портфелями: наиболее привлекательным является портфель с наибольшим математическим ожиданием (ожидаемой доходностью) и наименьшей дисперсией (риском), б) Функция полезности инвестора должна быть квадратичной:
Из формулы (1.43) следует: из двух портфелей с одинаковой ожидаемой доходностью инвестор выберет портфель с меньшей дисперсией; из двух портфелей с равной дисперсией - портфель с большей ожидаемой доходность. В заключение данного параграфа следует остановиться на вопросе, почему форма эффективной границы выпукла вверх. Если объединить в портфель две бумаги X и Y с корреляцией доходности +1, все возможные комбинации портфелей будут располагаться на прямой соединяющей их линии, как показано на рис. 1.26. В случае меньшей корреляции доходностей бумаг все возможные портфели (за исключением портфелей, состоящих только из бумаги X или бумаги Y) должны располагаться левее данной линии, поскольку их риск меньше риска любого портфеля с корреляцией +1. На рис. 1.26 при корреляции +1 доходности r1 соответствует портфель Р1, для меньшей корреляции – портфель Р1’; для доходности r2 при корреляции +1 соответствует портфель Р2, для меньшей корреляции - портфель Р2’ и т.д. Таким образом, если рассматривать две бумаги, все возможные комбинации портфелей должны располагаться или на прямой линии - для корреляции +1, или на выпуклой - при меньшей корреляции.
Допустим теперь, что точки X и Y на рис. 1.26 представляют собой не отдельные бумаги, а портфели. Каждый из них сформирован из нескольких бумаг. Эти портфели можно рассматривать как отдельные активы, поскольку они характеризуются определенной доходностью и риском. Если объединить их в один портфель, то получится такой же результат, как и в случае двух отдельных бумаг: все возможные комбинации новых портфелей будут располагаться на прямой линии при корреляции доходностей портфелей Хи Y +1 или левее данной линии при меньшей корреляции. Поскольку бумаги имеют обычно корреляцию меньше чем +1, то эффективная граница портфелей, составленная из большого количества бумаг, будет иметь выпуклую форму. На рис. 1.25 линия ВА имеет вогнутую форму. Такая конфигурация объясняется аналогичным образом, как и выпуклость эффективной границы. В данном случае разница состоит только в том, что актив (портфель) А характеризуется большим риском и меньшей ожидаемой доходностью по сравнению с портфелем В. Поэтому при корреляции их доходностей меньше чем +1 все возможные комбинации портфелей будут располагаться левее прямой линии, соединяющей данные активы, поскольку для каждого уровня ожидаемой доходности их риск меньше риска портфелей при корреляции +1.
|
||||||||||||
|
|
||||||||||||









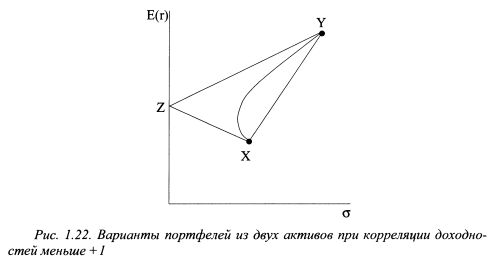

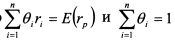 . Данный метод называется методом Марковца. Если накладывается условие не отрицательности уд. весов активов в портфеле, т.е. в. > 0, то это задача квадратичного программирования, т. к. в целевую функцию (1.42) уд. веса входят во второй степени. При возможности коротких продаж уд. веса активов могут быть отрицательными, и задача определения эффективных портфелей решается с помощью метода множителей Лагранжа.
. Данный метод называется методом Марковца. Если накладывается условие не отрицательности уд. весов активов в портфеле, т.е. в. > 0, то это задача квадратичного программирования, т. к. в целевую функцию (1.42) уд. веса входят во второй степени. При возможности коротких продаж уд. веса активов могут быть отрицательными, и задача определения эффективных портфелей решается с помощью метода множителей Лагранжа.
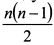 ковариаций. В результате для построения эффективной границы необходимо рассчитать
ковариаций. В результате для построения эффективной границы необходимо рассчитать 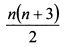 отдельных показателей ожидаемой доходности, дисперсий и ковариаций. Так, если мы определяем эффективную границу для портфеля из 5 активов, необходимо получить 20 исходных данных, для 10 активов - уже 65 данных, для 20 активов - 230 данных, а для 30 активов - 495 данных и т.д. Таким образом, большое количество вычислений делает модель Марковца не очень удобной для решения задачи определения эффективной границы. Данная проблема в более простой форме была решена в модели У.Шарпа, которая будет представлена в главе 3.
отдельных показателей ожидаемой доходности, дисперсий и ковариаций. Так, если мы определяем эффективную границу для портфеля из 5 активов, необходимо получить 20 исходных данных, для 10 активов - уже 65 данных, для 20 активов - 230 данных, а для 30 активов - 495 данных и т.д. Таким образом, большое количество вычислений делает модель Марковца не очень удобной для решения задачи определения эффективной границы. Данная проблема в более простой форме была решена в модели У.Шарпа, которая будет представлена в главе 3.