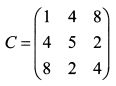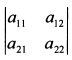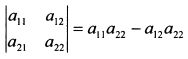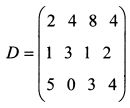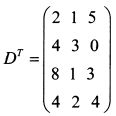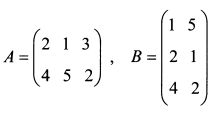|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
Приложение 4. Основы матричного исчисленияМатрицей называют прямоугольную числовую таблицу, состоящую из т строк и п столбцов. Числа, составляющие матрицу, называются ее элементами. Если обозначить элемент матрицы через atj, то это означает, что данное число а стоит на пересечении i-й строки j-го столбца матрицы. Матрицу обозначают как:
В матрице (П. 1.6) элемент ап согласно ее индексам i nj стоит соответственно на пересечении первой строки и первого столбца, элемент ап - на пересечении первой строки и второго столбца, элемент а2х - на пересечении второй строки и первого столбца и т.д. Данная матрица насчитывает т строк и п столбцов. Поэтому скажут, что это матрица типа или размера тхп. Матрицу как единый объект обычно обозначают заглавными латинскими буквами: А, В, Си т.д. Если матрица имеет только одну строку и п столбцов, ее называют матрицей-строкой:
или, опустив индекс j, так как у матрицы один столбец:
Если количество строк матрицы равно количеству ее столбцов, т.е. m = n, матрицу называют квадратной. Например, матрица
является квадратной. Элементы квадратной матрицы
Для квадратной матрицы выделяют такое понятие как определитель. У матрицы размера 2x2 определитель обозначают как:
Определитель равен:
Если в некоторой исходной матрице D столбцы заменить ее строками, то получится новая матрица, которую называют транспонированной к данной и обычно обозначают через DT. Пусть исходная матрица:
Транспонированная к ней матрица имеет вид:
При транспонировании первая строка матрицы D: 2 4 8 4 стала первым столбцом матрицы DT, вторая строка матрицы D: 1 3 1 2 - вторым столбцом матрицы DT и т.д. Если имеется матрица-строка, то транспонированной к ней будет матрица-столбец и наоборот. Таким образом, если исходная матрица имела m строк и п столбцов, то транспонированная будет насчитывать п строк и m столбцов. Матрицы можно перемножать. Однако для этого необходимо выполнение следующего условия. При умножении матрицы А на матрицу В количество столбцов матрицы А должно обязательно соответствовать количеству строк матрицы В, В противном случае умножение невозможно. Квадратные матрицы перемножаются между собой, поскольку у них количество строк и столбцов одинаковое. В результате умножения матрицы А на матрицу В получается матрица С. У нее элемент сг является суммой последовательного произведения элементов i-й строки матрицы А на элементы j-го столбца матрицы В. Пример.
Количество столбцов матрицы А равно количеству строк матрицы В, поэтому их можно перемножать:
Как видно из примера, после перемножения получается матрица, которая имеет такое же количество строк, что и первая и такое же количество столбцов, что и вторая.
|
||||||||||||
|
|
||||||||||||









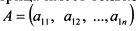 . Поскольку матрица имеет только одну строку, то индекс i у элементов матрицы можно опустить:
. Поскольку матрица имеет только одну строку, то индекс i у элементов матрицы можно опустить: 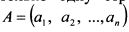 . Размер такой матрицы запишут как 1 х п. Если матрица имеет только один столбец и т строк, то это матрица-столбец:
. Размер такой матрицы запишут как 1 х п. Если матрица имеет только один столбец и т строк, то это матрица-столбец:
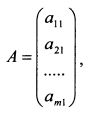
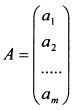
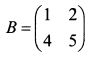
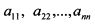 образуют главную диагональ. Для матрицы В главная диагональ представлена элементами 1 и 5. Квадратная матрица может быть симметрической. В этом случае симметричные относительно главной диагонали элементы равны. Например, матрица С является симметрической:
образуют главную диагональ. Для матрицы В главная диагональ представлена элементами 1 и 5. Квадратная матрица может быть симметрической. В этом случае симметричные относительно главной диагонали элементы равны. Например, матрица С является симметрической: