|
||||||||||||
|
||||||||||||
| Какой Форекс-брокер лучше? Альпари NPBFX FORTFS Сделай свой выбор! | ||||||||||||
| Какой брокер лучше? Альпари NPBFX FORTFS | ||||||||||||
Приложение 6. Определение геометрической формы границы МарковцаВ параграфе 1.2.10. было сказано, что график общей границы Марковца в координатах Ожидаемая доходность и риск портфеля равны:
Выразим уд. вес второго актива через первый:
Подставим значение в2 из (П. 1.13) в (П. 1.11) и найдем 01:
Подставим в равенство (П. 1.12) значение в2 из (П. 1.13) и 01 из (П. 1.14):
или
или
Уравнение (П. 1.15) описывает кривую второго порядка на плоскости в координатах В общей форме уравнение кривой второго порядка записывается как:
В уравнении (П. 1.16) первые три слагаемых имеют вторую степень относительно переменных х и у, и их сумма образует так называемую квадратичную форму:
Матрица данной квадратичной формы симметрическая и имеет вид:
В аналитической геометрии доказывается, что если определитель матрицы квадратичной формы (П. 1.17) отрицательный, то уравнение (П. 1.16) описывает фигуру гиперболического типа. В связи со сказанным составим квадратичную форму уравнения (П. 1.15) и найдем знак ее определителя. Квадратичная форма имеет вид:
Знаете ли Вы, что: участвуя в программе лояльности от Форекс-брокера NPBFX, Вы в зависимости от наторгованного Вами оборота можете получить в подарок iPad, iPhone, планшетный компьютер и даже автомобиль «BMW».
В уравнении (П. 1.18):
Определитель матрицы квадратичной формы (П. 1.18) равен:
В определителе (П.1.19) квадрат первой скобки есть число положительное. Вторая скобка при
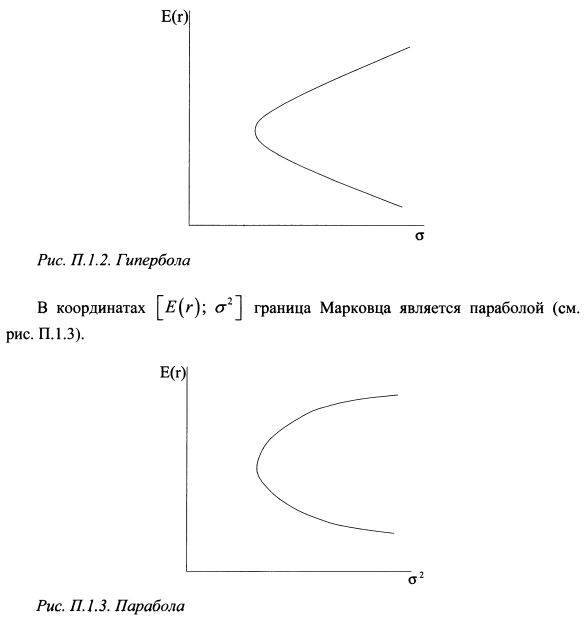
Когда граница Марковца строится на основе большого количества бумаг, то она представляет комбинацию большого количества соединенных между собой кусочков парабол. С помощью программы Excel легко построить график границы Марковца портфелей, состоящих из двух активов. Данный вопрос мы рассмотрим в Приложении 7.
|
||||||||||||
|
||||||||||||
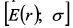представляет собой гиперболу. Докажем данное положение на примере портфеля, состоящего из двух активов.
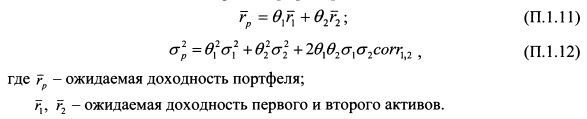
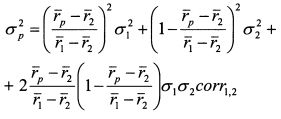
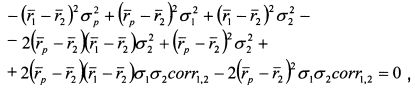
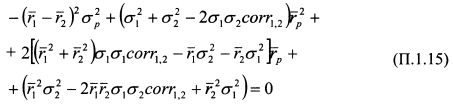
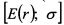. Переменными являются 
.
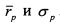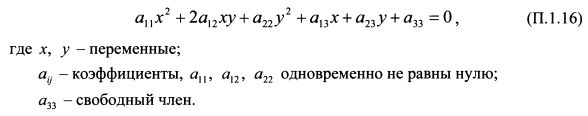
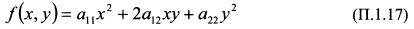
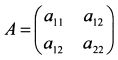
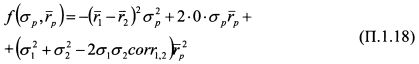
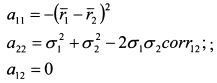
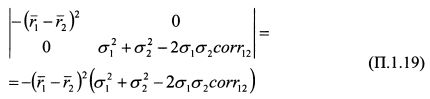
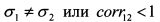также дает положительное число. Поэтому определитель квадратичной формы отрицателен. Это означает, что исходное уравнение (П. 1.15) является гиперболой. График гиперболы представлен на рис. П. 1.2.
