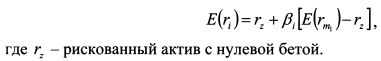|
||||||||||||
|
||||||||||||
| Какой Форекс-брокер лучше? Альпари NPBFX RoboForex Сделай свой выбор! | ||||||||||||
| Какой брокер лучше? Альпари NPBFX RoboForex | ||||||||||||
3.2.2. САРМ с нулевой бетойМодификацию САРМ для случая, когда отсутствует актив без риска, но имеется актив, содержащий только нерыночный риск, предложил Ф.Блэк. У актива только с нерыночным риском бета равна нулю. Для такой ситуации можно построить SML, которая будет проходить через рыночный портфель и рискованный актив с нулевой бетой. Уравнение САРМ в этом случае принимает вид:
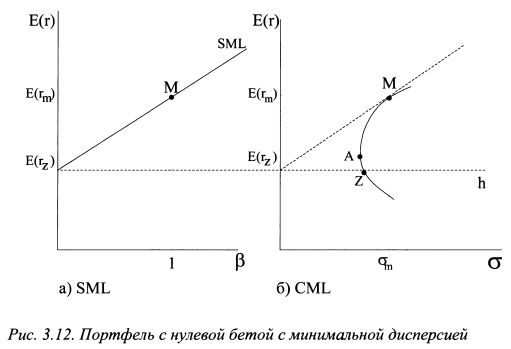
В качестве актива с нулевой бетой можно, например, рассматривать облигацию крупной компании. Если инвестор будет держать ее до погашения, то гарантирует себе определенный уровень процента, который не зависит уже от последующих колебаний цены этой бумаги. Единственный риск, которому подвергается вкладчик, это риск банкротства эмитента, поскольку в этом случае предприятие может и не осуществить причитающиеся ему платежи по облигациям. Знаете ли Вы, что: Вы можете выиграть от $20 до $250 в конкурсе «Formula FX» от Альпари, заняв призовые места с 1-го по 20-е. Для участия необходим реальный счет, пополненный не менее чем на $20. Победитель может снять призовую сумму в любой момент времени без каких-либо ограничений.
В качестве актива с нулевой бетой также можно представить портфель, состоящий из рискованных бумаг. Тогда характерной чертой данного портфеля должна быть короткая позиция по части активов. На границе Марковца в координатах МОЖНО найти портфель с нулевой бетой с минимальной дисперсией. На рис. 3.12а представлена SML для случая, когда отсутствует актив без риска. Поэтому SML проходит через рыночный портфель и актив без рыночного риска, ожидаемая доходность которого равна E(rz). На рис. 3.126 изображена граница Марковца. Портфель с нулевой бетой с минимальной дисперсией расположен на ней в точке Z. (Портфель А представляет собой портфель с минимальной дисперсией.) Коэффициент бета портфеля Z равен нулю. Следовательно, коэффициент корреляции доходности портфеля Z с доходностью рыночного портфеля также равен нулю. На рис. 3.12б на прямой Zh располагаются портфели с нулевой бетой. Поэтому корреляция их доходностей с рыночным портфелем равна нулю. |
||||||||||||
|
||||||||||||
