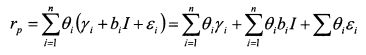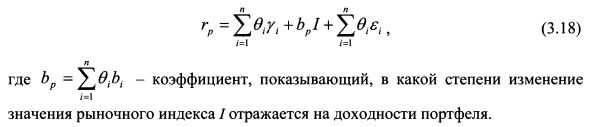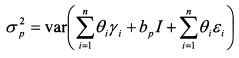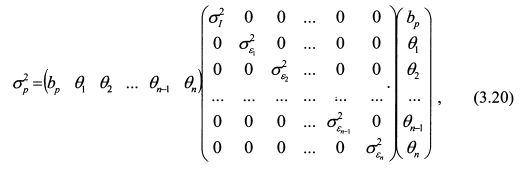|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
3.3. Модель У.Шарпа. 3.3.1. Диагональная модельОжидаемую доходность актива можно определить не только с помощью уравнения SML, но также на основе так называемых индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависят от ряда показателей, характеризующих состояние рынка, или индексов. Простая индексная модель была предложена У.Шарпом в середине 60-х годов. Цель ее разработки состояла в том, чтобы упростить процесс определения эффективной границы Марковца, сократив количество необходимых вычислений. У.Шарп назвал модель диагональной, В модели представлена зависимость между доходностью актива и значением рыночного индекса. Она предполагается линейной. Уравнение модели можно записать как:
Случайную компоненту доходности at можно разделить на две части:
yi является константой и представляет собой ожидаемую доходность актива при отсутствии воздействия на него рыночных факторов. ei - это собственно случайная величина со средним значением равным нулю. С учетом сказанного модель принимает вид:
где ?. - независимая случайная переменная (ошибка): она показывает специфический риск актива, который нельзя объяснить действием рыночных сил. Значение ее средней равно нулю, дисперсия постоянна, ковариация со значением рыночного индекса равна нулю; ковариация с нерыночным компонентом доходности других активов равна нулю, т.е. По условиям модели ожидаемое значение величины е. равно нулю. Поэтому на основе формулы (3.16) ожидаемое значение доходности актива E(ri) определяется как:
Модель получила название диагональной, поскольку риск портфеля можно представить с помощью ковариационной матрицы, в которой все значения равны нулю, кроме значений, расположенных на главной диагонали. Поясним сказанное. Доходность портфеля равна:
Подставим в формулу (3.17) формулу (3.16):
ИЛИ
На основе формулы (3.18) дисперсия доходности портфеля равна:
или
Формулу (3.19) можно записать в матричной форме как:
Из выражения (3.20) видно, что в ковариационной матрице по главной диагонали стоят дисперсия рыночного индекса и дисперсии специфических рисков активов портфеля. Остальные значения матрицы равны нулю.
|
||||||||||||
|
|
||||||||||||










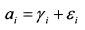

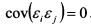 . В силу центральной предельной теоремы е. распределена нормально, поскольку на нее оказывает влияние большое количество разных факторов.
. В силу центральной предельной теоремы е. распределена нормально, поскольку на нее оказывает влияние большое количество разных факторов.