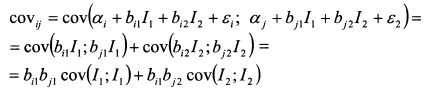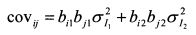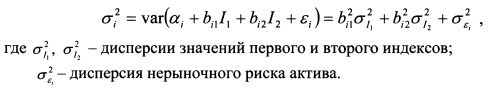|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
3.10. Многофакторные модели. 3.10.1. Принципы построения многофакторной моделиСуществуют финансовые инструменты, которые по-разному реагируют на изменение макроэкономических показателей. Например, доходность акций компаний, выпускающих автомобили, более чувствительна к общему состоянию экономики, а акций ссудосберегательных учреждений - к уровню процентных ставок. Поэтому в ряде случаев более точным может оказаться прогноз доходности актива на основе многофакторной модели, включающей несколько переменных, от которых зависит доходность данного актива. Выше мы представили модель Шарпа, которая является однофакторной. Ее можно превратить в многофакторную, если слагаемое J3trm представить в качестве нескольких слагаемых, каждое из которых является одной из макроэкономических переменных, определяющих доходность актива. Например, если инвестор полагает, что доходность акции зависит от двух составляющих - общего объема выпуска продукции и процентных ставок, то зависимость между ее доходностью и данными индексами примет вид:
Для определения ожидаемой доходности акции модель (3.35) следует использовать в форме:
В модели, представленной формулой (3.35), между индексами 1Х и /2 может наблюдаться некоторая корреляция. Данный факт не является помехой для использования ее в форме (3.36) при определении ожидаемой доходности акции. Однако может возникнуть необходимость получить модель (3.35) для случая не коррелируемости индексов. Это позволит, в частности, использовать более простой подход для нахождения эффективной границы портфелей, сократив число вычислений. Рассмотрим прием исключения коррелированности индексов в двухфакторной модели (3.35). На основе прошлых данных статистики построим регрессию индекса I2 на I1:
Выделим в уравнении (3.37) величину независимую от I1. Она представлена случайной переменной
или
Дальнейшее построение модели проведем для последнего случая, т.е. на основе равенства (3.39). Выразим из равенства (3.39) I2:
Подставим его значение в (3.35):
ИЛИ
ИЛИ
Уравнение (3.41) позволяет упростить процесс определения ковариаций активов. Поскольку индексы не коррелированы между собой, не коррелированы значения si и е} как между собой, так и с индексами, то ковариация i-го и j-го активов равна:
или
Соответственно риск актива как сумма независимых случайных величин составляет: |
||||||||||||
|
|
||||||||||||










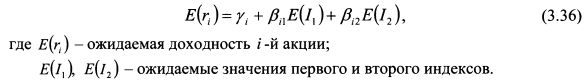

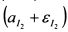 . Поэтому, если ее определить как второй индекс в уравнении (3.35), то он будет не коррелирован с индексом I1. Обозначим новый второй индекс как I'2. Он равен:
. Поэтому, если ее определить как второй индекс в уравнении (3.35), то он будет не коррелирован с индексом I1. Обозначим новый второй индекс как I'2. Он равен:
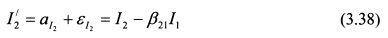 Из равенства (3.38) следует, что ожидаемое значение индекса I'2 равно аI2. Если
необходимо задать новый индекс с нулевым ожидаемым значением, то равенство (3.38) следует уменьшить на величину аI2:
Из равенства (3.38) следует, что ожидаемое значение индекса I'2 равно аI2. Если
необходимо задать новый индекс с нулевым ожидаемым значением, то равенство (3.38) следует уменьшить на величину аI2:
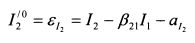
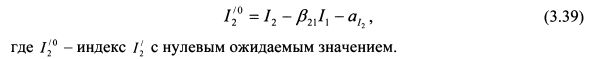
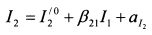
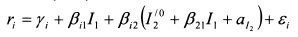
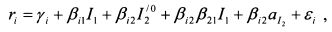
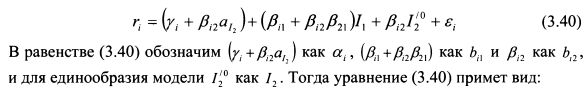
 В модели (3.41) индекс I1 - это прежний индекс выпуска продукции, индекс I2 представляет собой индекс разности между фактическими процентными ставками и ожидаемыми процентными ставками при данном ожидаемом значении индекса выпуска продукции I1. Соответственно коэффициент bi2 показывает степень реакции доходности акции к данному индексу. Его также можно определить как степень чувствительности доходности акции к изменению процентных ставок при фиксированном значении индекса выпуска продукции.
В модели (3.41) индекс I1 - это прежний индекс выпуска продукции, индекс I2 представляет собой индекс разности между фактическими процентными ставками и ожидаемыми процентными ставками при данном ожидаемом значении индекса выпуска продукции I1. Соответственно коэффициент bi2 показывает степень реакции доходности акции к данному индексу. Его также можно определить как степень чувствительности доходности акции к изменению процентных ставок при фиксированном значении индекса выпуска продукции.