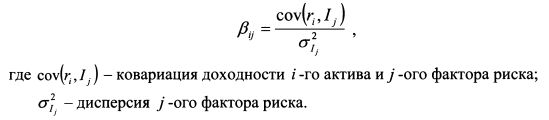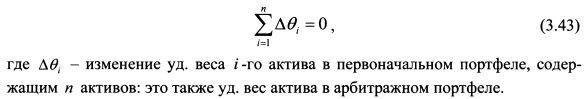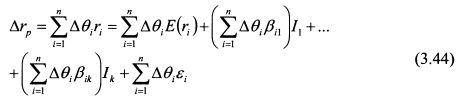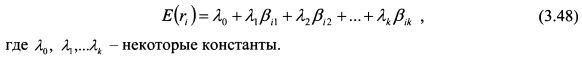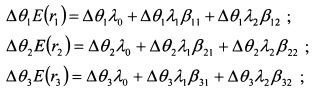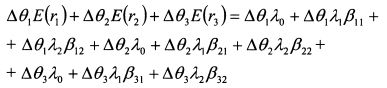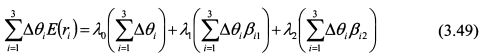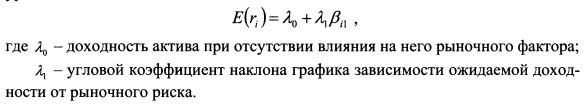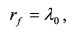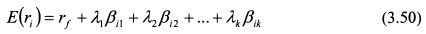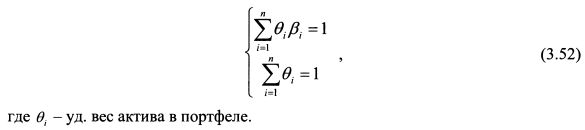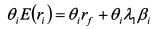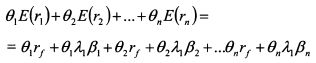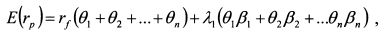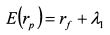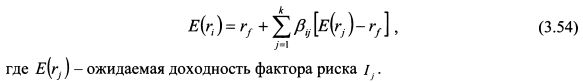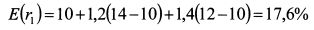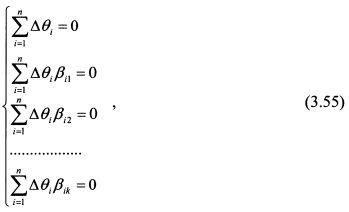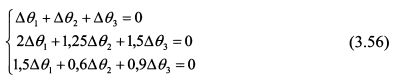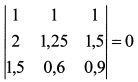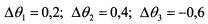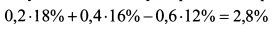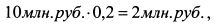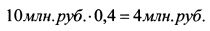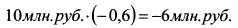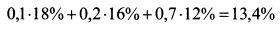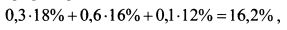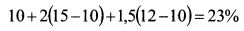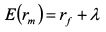3.11. Арбитражная модель Росса

В 1976 г. С.Росс предложил модель оценки доходности активов, которая получила название "Арбитражная теория оценки стоимости" (Arbitrage pricing theory - APT). В рамках модели все инвесторы имеют одинаковые ожидания относительно ожидаемой доходности активов и вероятностных распределений значений факторов риска, отсутствуют ограничения на короткие продажи. Как отмечают Р.Ролл и С.Росс, в качестве первого принципа модели выступает линейный процесс формирования доходности активов. В отличие от САРМ, в APT не делается акцент на какой-либо особый портфель, не учитывается положение об эффективности рыночного портфеля, не делаются особые предположения о функции полезности инвестора, а лишь предполагается ее монотонность и выпуклость. Модель не ограничивается одним временным периодом.

Свои рассуждения С.Росс начинает с предположения о том, что инвесторы считают: доходности активов определяются линейной моделью с к факторами риска:

Коэффициент чувствительности /? определяется как и в модели САРМ по формуле:

В модели предполагается, что количество активов на рынке намного больше количества факторов к, влияющих на доходность активов.

Модель получила название арбитражной, так как она накладывает арбитражные ограничения на доходности активов. Это означает, что в случае нарушения равновесия на рынке, т.е. возникновения нелинейных соотношений между риском и доходностью активов, можно заработать арбитражную прибыль. В свою очередь действия арбитражеров восстановят равновесие. Арбитражная прибыль получается в результате формирования арбитражного портфеля.

С.Росс рассматривает инвестора, который владеет некоторым портфелем и анализирует варианты создания различных арбитражных портфелей на его основе. Арбитражный портфель характеризуется тем, что его формирование не связано с дополнительными издержками, так как покупка одних активов финансируется за счет средств от продажи других активов в портфеле. Таким образом, в арбитражном портфеле сумма всех уд. весов активов равна нулю:

На основе уравнения (3.42) дополнительный доход, который инвестор получит от арбитражного портфеля, равен:

В уравнении (3.44) последнее слагаемое представляет собой специфический риск. Для широко диверсифицированного портфеля его значение практически равно нулю, поэтому им можно пренебречь.

По определению арбитражный портфель не должен быть восприимчив ни к одному фактору риска. Следовательно, удельные веса активов в портфеле можно подобрать для каждого фактора I_j таким образом, чтобы исключить и рыночный риск. Поэтому портфель характеризуется условием:

В результате, доходность, которую получит инвестор от формирования арбитражного портфеля при нарушении равновесия на рынке, определяется только первым слагаемым в уравнении (3.44) и составляет:

В условиях равновесия доходность арбитражного портфеля должна быть равна нулю, т.е.:

Условия (3.47), (3.45) и (3.43) определяют следующий вид зависимости ожидаемой доходности актива от факторов риска:

Чтобы увидеть данную зависимость, умножим уравнение (3.48) для каждого актива на значение его уд. веса Д0. в арбитражном портфеле и просуммируем полученные значения для всех активов. Для наглядности проделаем это для портфеля из трех активов при существовании двух факторов риска и, соответственно, двух коэффициентов чувствительности к факторам риска. Для каждого актива получаем результат:

Суммируем:

или

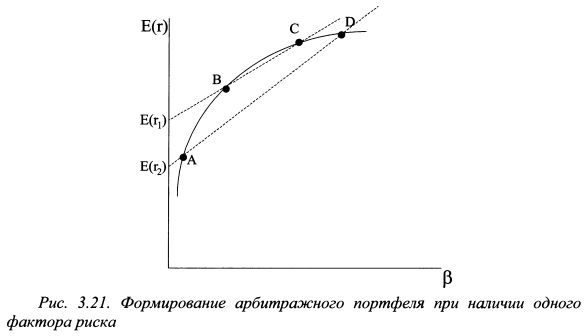
Если выполнены условия (3.43) и (3.45), то слагаемые в правой части (3.49) равны нулю, и, следовательно, выполняются зависимости (3.47) и (3.48). Зависимость (3.48) является центральным выводом модели APT,

Зависимость (3.48) можно получить и на основе стандартных рассуждений, не допускающих арбитражных ситуаций на рынке. Между риском и доходностью активов должна выдерживаться определенная закономерность. Поскольку нерыночный риск устраняется за счет диверсификации, то зависимость будет отражать только рыночный риск. Если зависимость между риском и доходностью активов не линейна, открывается возможность получить арбитражную прибыль. Проведем рассуждения для случая, когда доходности активов зависят только от одного фактора риска. Допустим, между доходностями активов и их рыночным риском, представленным коэффициентом бета, не выдерживается линейная зависимость. Пусть фактическая ситуация представлена на рис. 3.21, т.е. бумаги располагаются на некоторой кривой. Ожидаемые доходности портфелей и их риски, измеренные коэффициентом бета, являются средневзвешенными величинами. Поэтому инвестор может образовать два портфеля. Он осуществит короткую продажу бумаги С и купит бумагу В таким образом, чтобы доходность первого портфеля составила величину E(r₁). ОН также осуществит короткую продажу бумаги D и купит бумагу А таким образом, чтобы доходность второго портфеля составила величину E(r₂). После этого инвестор продаст менее доходный второй портфель и купит более доходный первый портфель. Арбитражная прибыль составит разницу между E(r₁) И E(r₂). Для корректности рассуждений необходимо учесть еще один момент. Если каждый портфель построен только из двух бумаг, то он характеризуется высоким нерыночным риском. Поэтому в рассмотренной ситуации следует формировать широко диверсифицированные портфели. Это можно сделать следующим образом.

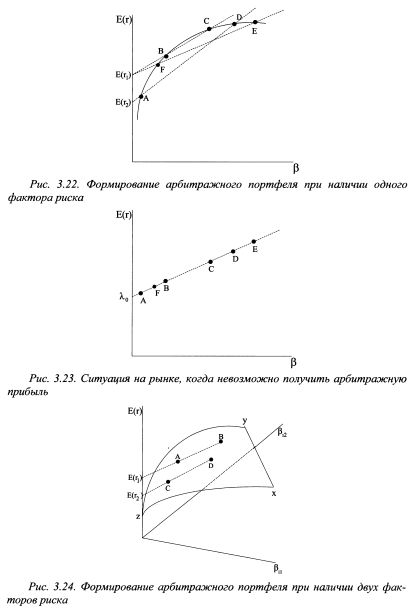
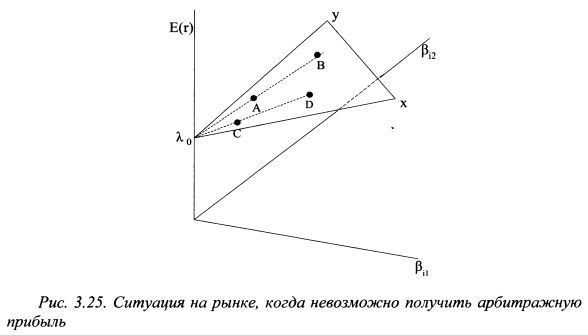
В первый портфель кроме бумаг В и С следует включить также бумаги F и Е, осуществив короткую продажу бумаги Е и купив на полученные средства бумагу F. Данная ситуация представлена на рис. 3.22. Поскольку на рынке зависимость между доходностями бумаг не линейная, то в первый портфель можно включить указанным способом и другие бумаги. Аналогичным образом можно добавить бумаги и во второй портфель. В результате получим широко диверсифицированные портфели. Участники рынка будут зарабатывать арбитражную прибыль до тех пор, пока все бумаги не расположатся на прямой линии, проходящей через все активы, как показано на рис. 3.23. Такое расположение активов возникнет за счет того, что продажи одних бумаг приведут к уменьшению их цены и, следовательно, росту ожидаемой доходности. Напротив, покупка других бумаг вызовет рост их цены и падение ожидаемой доходности. Поэтому ожидаемая доходность i-го актива должна быть представлена следующим уравнением:

Если доходности бумаг зависят от двух факторов риска, то графически активы будут расположены на поверхности. На рис. 3.24 изображена ситуация, когда можно заработать арбитражную прибыль, поскольку поверхность zyx имеет выпуклую форму. Поэтому инвестор сформирует первый портфель за счет короткой продажи бумаги В и покупки на полученные средства бумаги А. Второй портфель формируется за счет короткой продажи бумаги D и покупки бумаги С. Второй портфель продается и покупается первый более доходный портфель. Арбитражная прибыль равна разности между E(r₁) и E(R₂). Чтобы исключить специфический риск следует сформировать широко диверсифицированный портфель, как было показано выше в примере с одним фактором риска. В результате совершаемых операций выпуклая поверхность превратится в плоскую (см. рис. 3.25.)

Определим на основе формулы (3.48) доходность актива без риска. Поскольку коэффициенты бета для него равны нулю, то его доходность представлена выражением:

Подставив в формулу (3.48) вместо Я0 ставку без риска, получим:

Необходимо определить, что представляют собой оставшиеся коэффициенты Я. в уравнении (3.50). Проведем рассуждения для коэффициента Я1. Допустим, доходности активов определяются только одним фактором риска I_I. Тогда уравнение (3.50) принимает вид:

Объединим данные активы в широко диверсифицированный портфель. Уд. веса активов в портфеле определим таким образом, чтобы совокупная бета портфеля была равна единице, т.е. веса активов в портфеле найдем из системы уравнений:

Умножим правую и левую части равенства (3.51) для каждого актива на его уд. вес актива в портфеле:

Просуммируем все равенства:

ИЛИ

или, в силу условия (3.52),

Отсюда:

Таким образом, \ есть превышение доходности портфеля с коэффициентом чувствительности к фактору риска /, равному единице над ставкой без риска или премия за риск для данного портфеля или фактора риска. Соответственно ожидаемая доходность такого портфеля равна ожидаемой доходности фактора риска. В рассуждениях мы определили ^ для случая, когда доходность активов определяется только одним фактором риска. Это условие можно опустить. Тогда, чтобы получить уравнение (3.53), необходимо портфель сформировать таким образом, чтобы он оказался нейтральным к другим факторам риска. Для этого надо найти уд. веса бумаг в портфеле из системы уравнений:

На основе аналогичных рассуждений можно определить любые коэффициенты Л . Таким образом, Л - это премия за риск для фактора риска I_j.

С учетом равенства (3.53) формула (3.50) принимает вид:

С помощью формулы (3.54) можно определить ожидаемую доходность актива.

Пример.

Инвестор определяет ожидаемую доходность актива с помощью APT, в которую он включил два фактора. Ставка без риска равна 10%. Ожидаемая доходность первого фактора риска составляет 14%, второго фактора риска - 12%. Коэффициенты чувствительности к факторам риска актива 1,2 и 1,4. Тогда ожидаемая доходность актива равна:

Как было отмечено выше, если на рынке активы не получают оценки адекватной факторам риска, то можно заработать арбитражную прибыль, сформировав арбитражный портфель. Для этого необходимо найти удельные веса активов в портфеле. Их можно определить на основе условий (3.43) и (3.45), которые должны выполняться одновременно:

где k – количество факторов риска, учитываемых в модели. Определив удельные веса, их следует подставить в уравнение (3.46). Если получен положительный результат, то найденный портфель является арбитражным.

Пример.

Портфель инвестора состоит из трех активов, которые восприимчивы к двум факторам риска. Ожидаемая доходность первого фактора риска 15%, второго - 12%, ставка без риска - 10%. Коэффициенты чувствительности к факторам риска для первого актива равны соответственно 2 и 1,5, второго актива -1,25 и 0,6, третьего актива - 1,5 и 0,9. Ожидаемая доходность первого актива равна 18%, второго - 16%, третьего - 12%. Определить, можно ли получить арбитражную прибыль.

Решение.

Найдем уд. веса каждого актива в арбитражном портфеле, решив следующую систему уравнений:

Определитель матрицы линейных уравнений (3.56) равен нулю:

Поскольку матрица является однородной, то равенство ее определителя нулю говорит о том, что данная система имеет бесконечно много решений. Ранг матрицы равен 2, а порядок 3. Для решения такой системы выбирают количество независимых переменных, которое равно разности между порядком матрицы и ее рангом. Остальные переменные являются зависимыми и находятся на основе произвольно задаваемых значений независимых переменных. В нашем примере независимой переменной выступает соответственно только одна переменная. Пусть это будет значение Ав]. Зададим его равным 0,2. Тогда получим одно из возможных решений системы (3.56):

Определим ожидаемую доходность арбитражного портфеля:

Поскольку получен положительный результат, то данный портфель является арбитражным.

Допустим, что общая стоимость портфеля инвестора составляет 10 млн. руб., в том числе первого актива - 1 млн. руб., второго - 2 млн. руб., третьего -7 млн. руб. Для формирования арбитражного портфеля инвестору необходимо купить дополнительно первого актива на сумму:

второго актива на сумму:

и продать третий актив (об этом говорит знак минус) для финансирования данной стратегии на сумму:

Доходность первоначального портфеля инвестора составляла:

Доходность нового портфеля равна:

т.е. на 2,8% больше, как и было определено выше.

Таким образом, если инвестор полагает, что нерыночный риск портфеля будет незначительным, то он может повысить ожидаемую доходность портфеля за счет определения арбитражных возможностей. В результате возникшего дополнительного спроса на первый и второй активы их цены должны вырасти и, следовательно, ожидаемые доходности упасть. Напротив, цена третьего актива снизится вследствие увеличения его предложения на рынке, и его ожидаемая доходность возрастет.

Инвесторы будут стремиться воспользоваться арбитражными возможностями, поэтому вскоре цены и доходности финансовых активов установятся на равновесном уровне. Например, ожидаемая доходность первого актива согласно APT составит:

В заключение решения данной задачи вернемся еще раз к системе уравнений (3.56). Она являлась квадратной, так как количество уравнений соответствовало количеству неизвестных. Арбитражная модель предполагает формирование широко диверсифицированного портфеля. Поэтому количество неизвестных, т.е. уд. весов бумаг в арбитражном портфеле, будет превышать количество уравнений, которое, согласно системе (3.55), определяется количеством факторов риска плюс еще одно уравнение. Такая система имеет бесчисленное множество решений. Поэтому алгоритм ее решения такой же как и системы (3.56), т.е. определяется количество независимых переменных. Им задаются произвольные значения, и на их основе вычисляются значения зависимых переменных. Поскольку независимым переменным можно задавать любые веса, то, как было отмечено, возможно бесчисленное множество решений. Какое из них предпочесть. Так как задача состоит в максимизации ожидаемой доходности портфеля, то, согласно формальному подходу, следовало бы выбрать наибольшие положительные веса для активов с более высокой ожидаемой доходностью и наибольшие отрицательные веса для активов с наименьшей ожидаемой доходностью, чтобы за их счет приобрести первые активы. Например, если бы в нашей задаче инвестор полностью продал менее доходный третий актив, т.е. задал его уд. вес равным минус один, то первый актив следовало бы купить в уд. Весе 0,33, а второй 0,67. Тогда ожидаемая доходность арбитражного портфеля составила бы 4,67%. Является ли такое решение оптимальным. Разумеется нет. По условиям модели портфель должен быть максимально диверсифицирован, чтобы исключить специфический риск. Если мы уменьшаем степень диверсификации, то увеличиваем нерыночные риски. В последнем случае мы исключили третью бумагу и добавили первую и вторую. В результате возросли связанные с ними диверсифицируемые риски. Поэтому при корректировке состава первоначального портфеля существуют ограниченные возможности варьирования уд. весами активов, чтобы портфель не стал обладать существенным специфическим риском.

Определенным недостатком модели является то, что в ней не выделены конкретные риски, которые необходимо учитывать. Р.Ролл и С.Росс провели проверку модели на основе ежедневных данных для акций, обращавшихся на Нью-Йоркской и Американской фондовых биржах за период с июля 1962 по декабрь 1972 года. Акции были объединены в алфавитном порядке в группы из 30 штук. Всего было образовано 42 группы. Они определили, что большая часть совместного изменения доходностей акций определяется четырьмя или пятью факторами риска.

В другом исследовании Н.Чен, Р.Ролл и С.Росс предположили, что на доходности бумаг должны влиять факторы, от которых зависят будущие доходы компаний, и факторы, определяющие ставку дисконтирования данных доходов. На этой основе они выделили четыре фактора: темп прироста ВНП, темп инфляции, спрэд между доходностями кратко- и долгосрочных облигаций США, спрэд между доходностями корпоративных облигаций с низким и высоким рейтингом.

Росс утверждает, что APT и САРМ - это разные по своему принципу модели. Однако можно сказать, что САРМ представляет собой частный случай APT. Это можно показать следующим образом. Если предположить, что доходности бумаг зависят только от одного фактора - рыночного портфеля, то уравнение (3.50) примет вид:

Умножим правую и левую части уравнения (3.57) для каждой бумаги на ее уд. вес в рыночном портфеле и суммируем уравнения для всех бумаг. Получим:

ИЛИ

Подставим значение Л из уравнения (3.58) в (3.57):

Уравнение (3.59) есть не что иное как уравнение SML модели САРМ.

С точки зрения теоретического подхода APT дает ключ к объяснению аномалий, которые были обнаружены на рынке в связи с проверкой САРМ, т.е. при оценке стоимости активов следует учитывать не просто доходность рынка, как предлагается САРМ, а ряд факторов.

APT дает инструментарий для определения арбитражных возможностей при формировании портфеля. Однако САРМ также обладает арбитражным потенциалом, который представлен величиной альфа. Если альфа активов в рамках модели САРМ не равна нулю, то существует потенциальная возможность заработать арбитражную прибыль.

Практическая значимость APT возникает в случае формирования портфеля, ориентированного на какие-либо определенные факторы риска, поскольку модель позволяет лучше учесть их в прогнозах и действиях инвестора. Например, в преддверии изменения некоторого макроэкономического фактора можно в большей степени сделать акцент на операции с активами, которые характеризуются более высоким коэффициентом чувствительности к этому фактору риска. В целом, однако, можно сказать, что APT не получила широкого распространения на практике.

Содержание

Далее