|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
Приложение 1. Вывод уравнения SMLУравнение SML можно вывести на основе максимизации функции полезности инвесторов в условии равновесия на финансовом рынке при данном бюджетном ограничении. Условие равновесия означает, что спрос на ценные бумаги равен их предложению по существующим ценам с учетом риска бумаг, и инвесторы могут занимать и размещать средства под ставку без риска. Сумма всех занимаемых и предоставляемых в кредит средств равна нулю, поскольку в условиях равновесия количество капиталов, которые хотят занять инвесторы и предоставить в кредит, одинаково. В рамках САРМ функция полезности k-го инвестора зависит от ожидаемой доходности и риска его портфеля, т.е. ее можно записать как:
Бюджетное ограничение сводится к использованию им всех собственных и доступных средств с учетом заимствования и кредитования. Стандартным методом решения оптимизационной задачи на максимизацию является метод множителей Лагранжа. Искусственно создается и максимизируется функция Лагранжа вида:
На рынке действует п инвесторов, обращается т рискованных ценных бумаг и безрисковый долг, обозначим его как f. Общая капитализация рынка равна Рт , стоимость портфеля к -го инвестора - Рк , стоимость i-й бумаги в портфеле k-го инвестора - Р.к 9 стоимость безрискового долга к -го инвестора в форме заимствования или кредитования - Р#. Обозначим уд. вес i-й бумаги k-го инвестора в общей капитализации рынка через в1к 9 уд. вес безрискового долга k-го инвестора в форме заимствования или кредитования в общей капитализации рынка через #д и уд. вес портфеля k-го инвестора в общей капитализации рынка через gk. Тогда:
Отсюда уд. веса i-й бумаги и безрискового долга в портфеле k-го инвестора равны:
Ожидаемая доходность портфеля k-го инвестора составляет:
Риск портфеля k-го инвестора равен:
Бюджетное ограничение инвестора состоит в использовании им всех доступных средств с учетом заимствования и кредитования, т.е. сумма всех уд. весов активов в портфеле должна быть равна единице:
Составим функцию Лагранжа:
Найдем частные производные уравнения (П.3.6) по 0ik:
На основании равенств (П.3.3) и (П.3.4) найдем производные
и
Подставим значения производных из (П.3.8) и (П.3.9) в (П.3.7):
Найдем частные производные уравнения (П.3.6) по в ^ :
На основании равенств (П.3.3) и (П.3.4) найдем производные
и
Подставим производные из (П.3.12) и (П.3.13) в (П.3.11):
Вычтем из уравнения (П.3.10) уравнение (П.3.14):
или
Уравнение (П.3.15) должно выдерживаться в условиях равновесия для всех бумаг и всех инвесторов, поскольку оно определено на основе максимизации их функции полезности. Уравнение (П.3.15) можно записать как:
Равенство (П.3.16) выполняется для каждой бумаги, поэтому для каждой пары бумаг i и c справедливо соотношение:
или после сокращении одинаковых множителей:
Просуммируем по всем инвесторам равенство (П.3.17), левую часть равенства относительно бумаги i, а правую - бумаги c. Поскольку оно выполняется для всех бумаг и инвесторов, то равенство сохранится и для суммы. Сумма в по всем инвесторам даст уд. вес j-й бумаги в капитализации рынка. Обозначим его через
Умножим числитель и знаменатель правой части формулы (П.3.18) на со:
Просуммируем правую часть равенства (П.3.19) по всем бумагам:
Значение дроби
после суммирования осталось таким же как и дроби
Поэтому приравняем их друг к другу:
В выражении (П.3.23)
Подставим правую часть формулы (П.3.24) в формулу (П.3.23):
В формуле (П.3.25)
Преобразуем его к виду:
Отношение
Равенство (П.3.27) является уравнением SML модели САРМ.
|
||||||||||||
|
|
||||||||||||









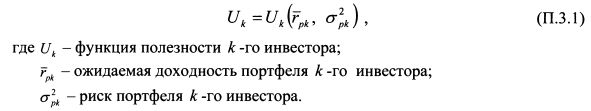
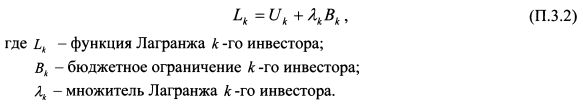
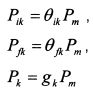
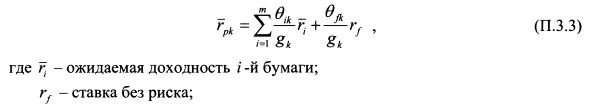
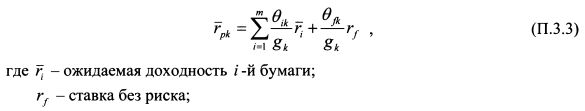
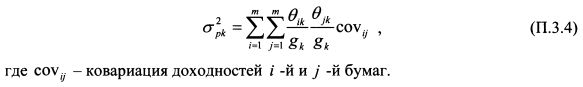

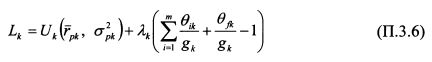
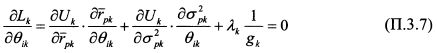
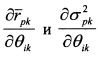 :
:

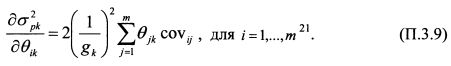
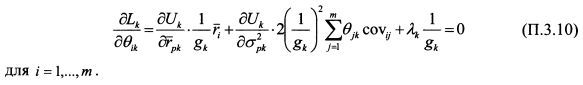
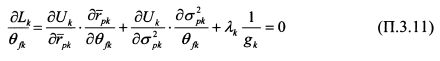
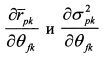 :
:


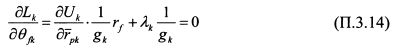
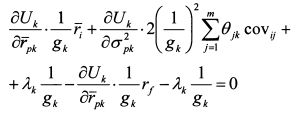
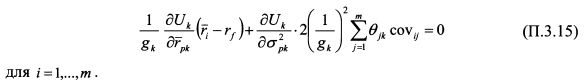
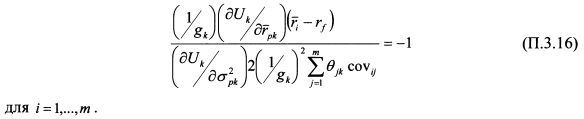
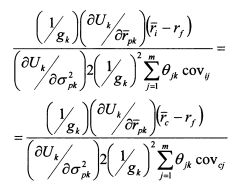
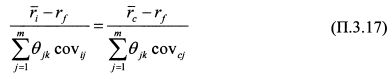
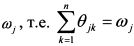 . После суммирования получим:
. После суммирования получим:
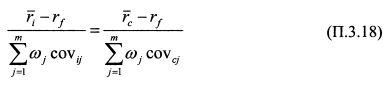
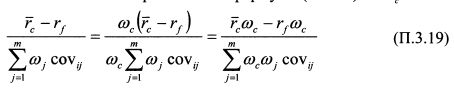





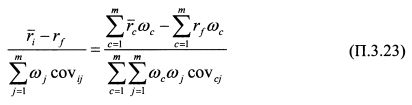
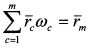 , т.е. равно ожидаемой доходности рыночного портфеля, а величина
, т.е. равно ожидаемой доходности рыночного портфеля, а величина 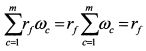 , поскольку сумма всех уд. весов ценных бумаг в экономике
, поскольку сумма всех уд. весов ценных бумаг в экономике 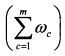 равна единице. Величина
равна единице. Величина 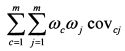 есть не что иное как дисперсия рыночного портфеля
есть не что иное как дисперсия рыночного портфеля 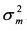 . Поэтому:
. Поэтому:
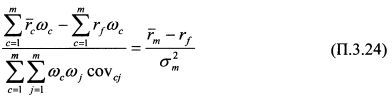
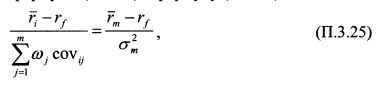
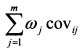 есть не что иное как ковариация доходности i-й бумаги с доходностью рынка, т.е. covim. Подставим это значение в равенство (П.3.25):
есть не что иное как ковариация доходности i-й бумаги с доходностью рынка, т.е. covim. Подставим это значение в равенство (П.3.25):
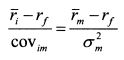
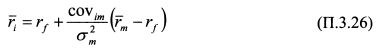
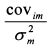 – это коэффициент бета i-й бумаги. Соответственно формула (П.3.26) принимает вид:
– это коэффициент бета i-й бумаги. Соответственно формула (П.3.26) принимает вид:
