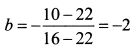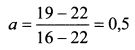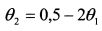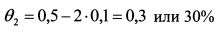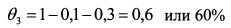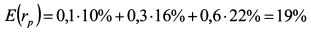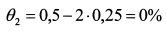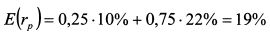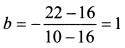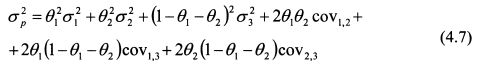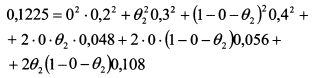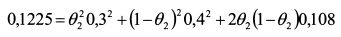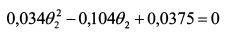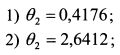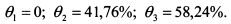|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
ГЛАВА 4. ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОЙ ГРАНИЦЫ И ОПТИМАЛЬНЫХ ПОРТФЕЛЕЙ. 4.1. Определение эффективной границы с помощью кривых изосредних и изодисперсий. 4.1.1. Эффективная граница при невозможности коротких продажНастоящая глава посвящена способам определения оптимальных портфелей и эффективной границы. Вначале мы рассмотрим графический подход определения эффективной границы, предложенный Г.Марковцем, после этого приведем метод множителей Лагранжа определения эффективной границы Г.Марковца и рыночного портфеля при возможности коротких продаж. В заключение остановимся на использовании метода линейного программирования. Метод нахождения эффективной границы был предложен Г.Марковцем в статье "Portfolio Selection". Он представил графическую иллюстрацию метода для портфелей, состоящих из трех активов, для условий, когда короткие продажи невозможны. Рассмотрим рассуждения Г.Марковца. Ожидаемая доходность портфеля из трех активов равна:
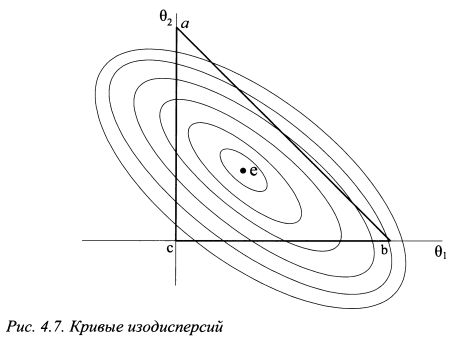
Риск портфеля составляет:
Сумма всех уд. весов равна единице:
Выразим уд. вес третьего актива из формулы (4.3):
и подставим его в формулу (4.1):
или
Формула (4.5) показывает, что ожидаемая доходность портфеля является функцией двух переменных: вх и в2. Если подставить значение в3 из формулы (4.4) в формулу (4.2), то риск портфеля также будет функцией двух переменных: вх и в2. Поэтому графически решение задачи определения эффективной границы можно представить в двухмерном пространстве.
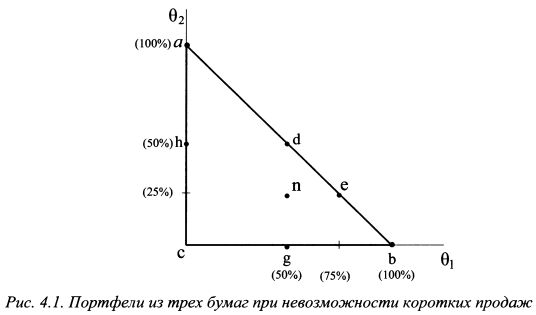
Рассмотрим рис. 4.1. По горизонтальной оси откладывается уд. вес первого актива, по вертикальной - второго. Все возможные комбинации портфелей представлены в рамках треугольника abc. Если все средства инвестированы в первый актив, то портфель расположен в точке b, если во второй, - в точке a. На прямой ab находятся портфели, состоящие только из первого и второго активов. Например, в точке d 50% средств инвестировано в первую бумагу и 50% во вторую, в точке е 15% средств приходится на первую бумагу и 25% на вторую. В точке с портфель состоит только из третьей бумаги. В точке g в него входит на 50% первая бумага и на 50% третья. В точке h он состоит на 50% из второй и на 50% из третьей бумаги. В точке п 50% средств приходится на первую бумагу, 25% на вторую и 25% на третью. Портфели, которые располагались бы ниже горизонтальной оси недоступны инвестору, так как нарушается условие в2 > 0, недоступны портфели и левее вертикальной оси, поскольку это противоречит условию вх > 0. Соответственно недоступны портфели, расположенные выше и правее прямой ab, которая задается уравнением 1 - вх - в2 = 0, так как должно выдерживаться ограничение 0Ъ = 1 - вх - в2 > 0, т.е. уд. вес третьей бумаги не может быть отрицательным. Таким образом, все возможные комбинации портфелей с использованием всех средств инвестора и невозможности коротких продаж располагаются в рамках треугольника abc. Кривую, на которой расположены портфели с одинаковой ожидаемой доходностью, Г.Марковец называет изосредней кривой доходности (isomean curve); кривую для портфелей с одинаковой дисперсией - линией изодисперсии (isovarience line). Графически изосредние кривые представляют собой набор параллельных прямых линий. Данный вывод можно получить на основе уравнения (4.5). Выразим из данного уравнения уд. вес второй бумаги при
Уравнение (4.6) есть уравнение прямой линии вида:
Угол наклона функции (4.6) есть величина постоянная. Поэтому, если изменять ожидаемую доходность портфеля Пример 1. Ожидаемая доходность первой бумаги равна 10%, второй - 16%, третьей 22%. Инвестор хотел бы сформировать портфель с ожидаемой доходностью 19%. Угол наклона изосредней линии равен:
Коэффициент а составляет:
Формула изосредней линии для портфеля с ожидаемой доходностью 19% имеет вид:
Портфель с доходностью 19% можно получить, придав разные уд. веса активам. Пусть первую бумагу инвестор включает в портфель в уд. весе 10%. Тогда уд. вес второй бумаги должен составить:
Уд. вес третьей бумаги в портфеле согласно уравнению (4.4) составит:
Ожидаемая доходность портфеля равна:
Портфель с доходностью 19% можно получить и на основе других сочетаний уд. весов. Пусть первую бумагу инвестор включает в портфель в уд. весе 25%. Тогда уд. вес второй бумаги составит:
Это означает, что вторая бумага в портфель не включается. Оставшаяся сумма средств инвестируется в третью бумагу. Ожидаемая доходность такого портфеля равна:
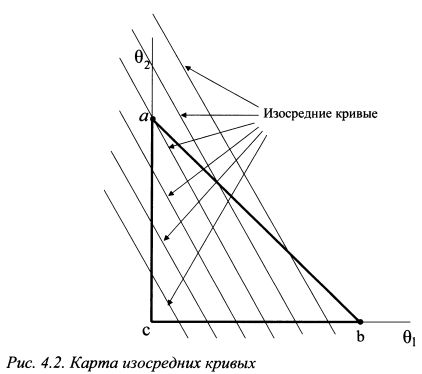
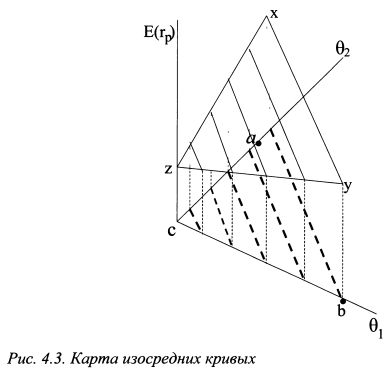
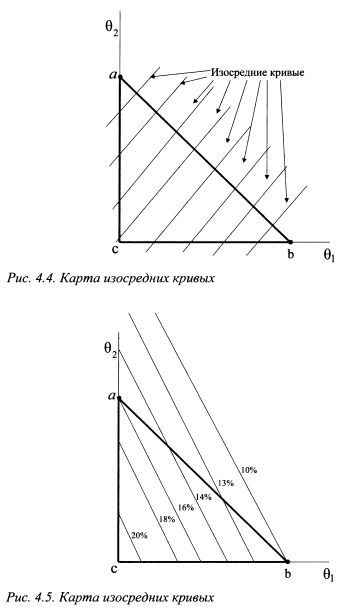
На рис. 4.2 карта изосредних кривых является не чем иным как проекцией линий уровня. Они изображены на рис. 4.3. Данный рисунок представляет собой трехмерное пространство. В горизонтальной плоскости расположены оси вх и в2 9 т.е. уд. веса первого и второго активов. Вертикальная ось - это ось ожидаемой доходности портфеля. Ожидаемая доходность портфеля есть функция переменных вх и в2. Разные сочетания уд. весов активов дают плоскость xyz. Если разрезать ее параллельными плоскостями, перпендикулярными оси E(RP), то получим на данной плоскости параллельные линии, которые соответствуют определенной фиксированной ожидаемой доходности портфеля для разных комбинаций уд. весов в портфеле. Проекции данных линий на горизонтальную плоскость 6хс62 и представляют собой изосредние кривые. На графике они изображены толстыми пунктирными линиями. На рис. 4.2 и 4.3 изосредние кривые имеют отрицательный наклон. Однако он может быть и положительным, как представлено на рис. 4.4. Динамика роста ожидаемой доходности портфеля также может идти в любом направлении, например, на рис. 4.2 как от точки с к прямой аb так и наоборот. На рис. 4.4 это может быть как направление от точки а к точке b, так и наоборот. Наклон графика, а также направление роста ожидаемой доходности зависят от значений ожидаемой доходности активов, которые располагаются в точках а и b. Поясним сказанное на цифрах из примера 1.
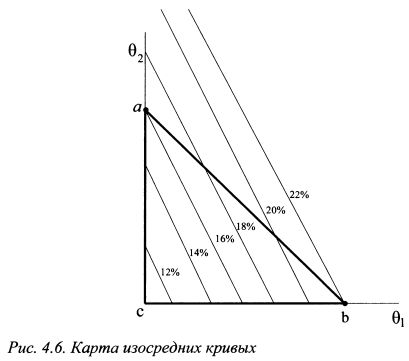
В примере коэффициент b отрицателен, поэтому наклон изосредних кривых соответствует рис. 4.5, а увеличение доходности идет по направлению от линии ab к точке с. Если в примере 1 изменить доходности бумаг следующим образом: доходность первой 22%, второй 16%, третьей 10%, то увеличение доходности будет идти от с в направлении ab (см. рис.4.6) при угловом коэффициенте равным -2.
Изменим еще раз доходности бумаг: доходность первой 22%, второй 10%, третьей 16%. Тогда угол наклона изосредних линий станет положительным:
График изосредних соответствует рисунку 4.4, и доходность изосредних возрастает в направлении от а к b. Если же доходности бумаг равны: первой 10%, второй 22% и третьей 16%, то на рис. 4.4 доходность возрастает от Ь к а при угловом коэффициенте равным единице.
Кривая изодисперсии представляет собой эллипс. На данной кривой расположены все портфели с одинаковой дисперсией. Соответственно портфели с разными дисперсиями образуют семейство эллипсов, как показано на рис. 4.7. В точке е расположен портфель с минимальной дисперсией. Чем дальше расположен эллипс от точки е, тем большей дисперсией он характеризуется. На рис. 4.7 эллипсы расположены в направлении с северо-запада на юго-восток. Однако, как и в случае с изосредними кривыми, они могут принять и другие направления. Это зависит от расположения на графике бумаг, входящих в портфель. Кривую изодисперсии для каждого данного уровня дисперсии портфеля можно найти на основе формулы (4.7):
Она получается подстановкой в формулу (4.2) формулы (4.4). Задавая разные уд. веса в формуле (4.7) для данного уровня дисперсии, можно построить эллипс изодисперсии, на котором расположены портфели одинакового уровня риска.
Пример 2. Стандартное отклонение первой бумаги (в десятичных значениях) равно 0,2, второй бумаги 0,3, третьей 0,4. Ковариация первой и второй бумаг составляет 0,048, первой и третьей - 0,056, второй и третьей - 0,108. Инвестор хотел бы определить уд. веса второй и третьей бумаг в портфеле с дисперсией 0,1225, если уд. вес первой бумаги равен нулю. Решение. Запишем уравнение (4.7):
или
или
Решение данного уравнения дает значения в2:
В первом случае, чтобы получить портфель с дисперсией 0,1225, необходимо купить вторую бумагу в уд. весе 41,76% и третью в уд. весе 58,24%. Таким образом уд. веса активов в портфеле равны:
Второе значение в2 предполагает необходимость купить ее в уд. весе 264,12%. Чтобы получить такой уд. вес следует финансировать покупку второй бумаги за счет продажи третьей. Уд. веса активов в портфеле равны:
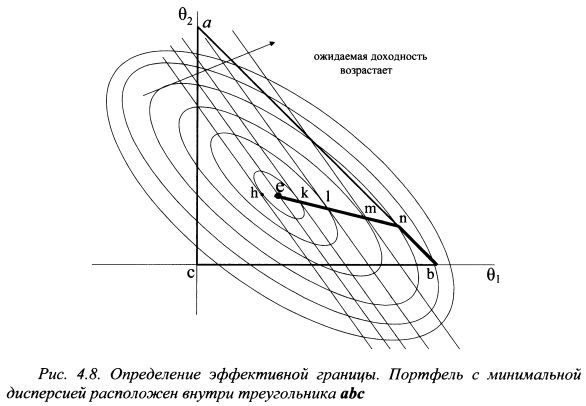
В примере 2 мы определили два портфеля с дисперсией 0,1225 и получили таким образом две точки эллипса изодисперсии. Подставив другое значение уд. веса первой бумаги, получим уд. веса еще для двух портфелей и, соответственно, еще две точки данного эллипса изодисперсии. Повторив данную операцию много раз, построим эллипс для портфелей с дисперсией 0,1225. Аналогичным образом найдем эллипсы изодисперсии и для портфелей с другими дисперсиями. Аналогично рис. 4.3 можно изобразить дисперсии портфелей в трехмерном пространстве. Тогда по вертикальной оси вместо ожидаемой доходности следует отложить дисперсию. В результате получим некоторую поверхность - эллиптический параболоид, на котором расположены дисперсии портфелей. Если провести плоскость перпендикулярную вертикальной оси, то она разрежет данную поверхность. Проекция полученной фигуры на горизонтальную плоскость будет не чем иным как эллипсом изодисперсии. Таким образом, эллипсы изодисперсии как и изосредние кривые являются линиями уровня. Чтобы определить эффективную границу, необходимо на одном графике совместить изосредние кривые и эллипсы изодисперсии (см. рис. 4.8). Для каждого данного уровня ожидаемой доходности портфели с минимальной дисперсией должны располагаться в точках касания соответствующей изосредней кривой и эллипса изодисперсии. Вначале Г.Марковец рассматривает случай, когда портфель с минимальной дисперсией лежит внутри треугольника abc. На рис. 4.8 доходность изосредних кривых возрастает слева направо, поэтому эффективными являются портфели е, А, /, т. Портфель е - это портфель с минимальной дисперсией. Портфели А, /, т расположены в точках касания эллипсов изодисперсии и соответствующих изосредних линий. На данном рисунке эффективные портфели расположены вправо, считая от портфеля е, поскольку доходность изосредних возрастает слева направо. Портфели, расположенные в точках касания изосредних и изодисперсии левее точки е, не могут быть эффективными, так как для каждого уровня дисперсии их ожидаемые доходности меньше соответствующих эффективных портфелей. Например, портфель h не является эффективным, поскольку его дисперсия равна дисперсии портфеля А, (они расположены на одном эллипсе изодисперсии), но ожидаемая доходность ниже. Эффективные портфели расположены на линии еп. Г.Марковец назвал ее критической линией (critical line). Она проходит через точки касания изосредних и изодисперсии и представляет собой прямую. Критическая линия является прямой, так как для всех эллипсов изодисперсий точкой симметрии является точка е, т.е. портфель с минимальным риском, и все они расположены симметрично относительно друг друга в одном направлении. Тот факт, что критическая линия является прямой, приводит к следующему выводу: объединение любого количества эффективных портфелей в один портфель вновь даст эффективный портфель.
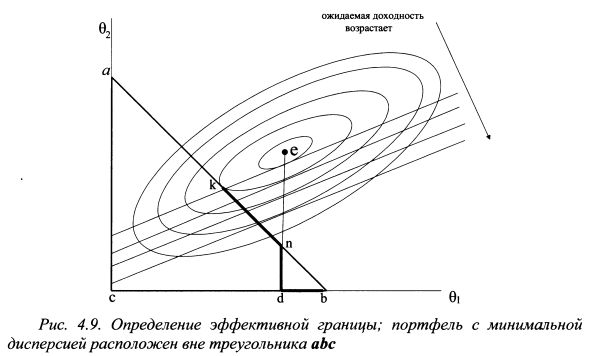
На рис.4.8 эффективная граница представлена прямой еп. Точка п лежит на границе ab. Поскольку уд. веса активов в портфеле не могут быть отрицательными, то оставшаяся часть эффективной границы представляет собой отрезок nb. Таким образом, на рис. 4.8 эффективная граница представлена ломаной епb. Рис. 4.9 представляет иллюстрацию Г.Марковцем случая, когда портфель с минимальной дисперсией лежит вне треугольника abc. Критической линией является прямая ed. Эффективные портфели расположены на прямой кп, далее на отрезке критической линии nd, так как она состоит из точек касания изосредних и изодисперсий, и отрезка db. Таким образом, эффективные портфели представлены ломаной линией kndb. |
||||||||||||
|
|
||||||||||||











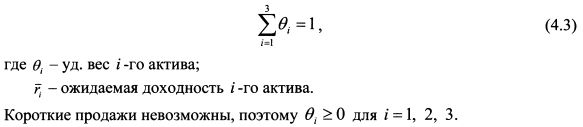

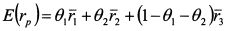
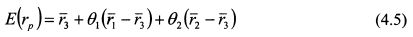
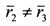 :
:
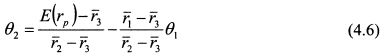

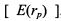 , то график функции будет смещаться параллельно вверх или вниз. В результате получим карту изосредних кривых как показано на рис. 4.2.
, то график функции будет смещаться параллельно вверх или вниз. В результате получим карту изосредних кривых как показано на рис. 4.2.