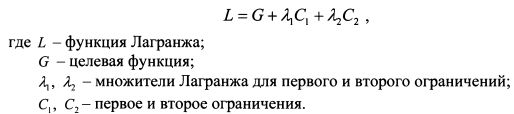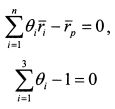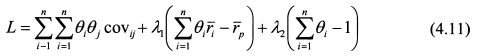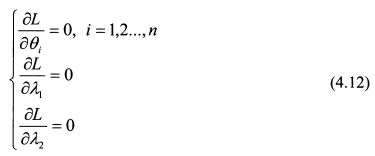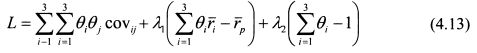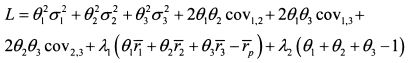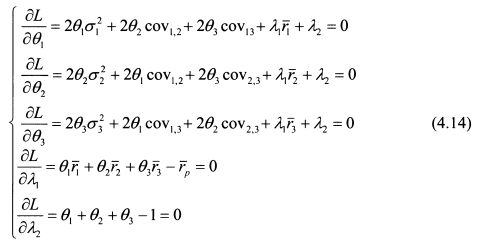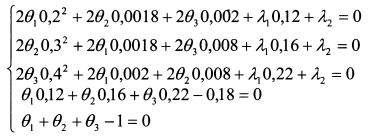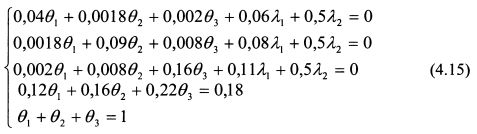4.2. Определение эффективной границы Марковца методом множителей Лагранжа

Для случая, когда короткие продажи активов разрешены, аналитически эффективную границу можно найти с помощью метода множителей Лагранжа. Задача сводится к минимизации дисперсии портфеля (а2):

при двух ограничивающих условиях: 1) ожидаемая доходность портфеля (r_p) равна:

2) сумма уд. весов всех активов равна единице:

Искусственно создается и минимизируется функция Лагранжа в форме:

Целевая функция представлена функцией (4.8), Первое ограничение - равенством (4.9), второе - (4.10). В функцию Лагранжа первое и второе ограничения включаем в следующей форме:

В общем виде функция Лагранжа запишется как:

Найдем частные производные функции (4.11) по 0Х,, Я^, Я2 и приравняем их к нулю:

Решение системы уравнений (4.12) дает ответ на вопрос, в каких уд. весах необходимо включить бумаги в портфель, чтобы он являлся эффективным, т.е. имел минимальную дисперсию для заданного уровня ожидаемой доходности. Следует подчеркнуть, что в рассмотренном виде решение дается для ситуации, когда короткие продажи разрешены.

Поясним представленный алгоритм определения эффективного портфеля на примере для трех бумаг.

Пример.

Стандартное отклонение доходности первой акции (в десятичных значениях) равно 0,2, второй - 0,3, третьей - 0,4. Ковариация доходностей первой и второй бумаг составляет 0,0018, первой и третьей - 0,002, второй и третьей - 0,008. Доходность первой бумаги (в десятичных значениях) составляет 0,12, второй - 0,16, третьей - 0,22. Определить уд. веса бумаг в портфеле с доходностью 0,18.

Решение.

Составим функцию Лагранжа:

Запишем ее в развернутом виде:

Найдем частные производные функции Лагранжа согласно системе (4.12):

Подставим в систему уравнений (4.14) цифровые значения задачи:

или

систему уравнений (4.15) получим:

Таким образом, портфель с минимальной дисперсией для ожидаемой доходности 18% должен состоять на 18,67% из первой бумаги, 35,56% второй бумаги и 45,77% третьей бумаги.

Содержание

Далее