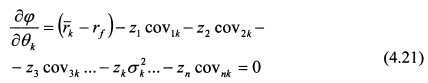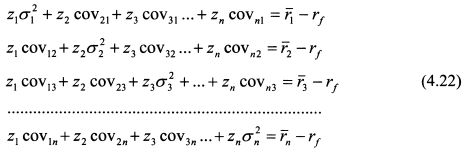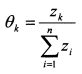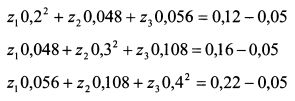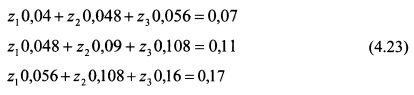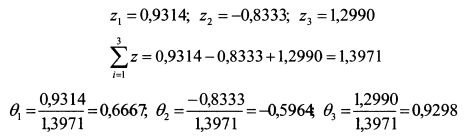|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
4.4. Определение рыночного портфеля при возможности заимствования и кредитованияПри возможности заимствования и кредитования эффективная граница превращается в прямую линию, касательную к эффективной границе Марковца, как показано на рис. 4.17. Обозначим ее через Н. Она проходит через две точки: ставку без риска и рыночный портфель М, Чтобы найти портфель Л/, необходимо рассчитать уд. веса входящих в него активов. Решить задачу можно следующим образом. Рыночный портфель расположен на касательной к эффективной границе Марковца. Это значит, что угол наклона линии Н к горизонтальной оси графика является наибольшим по сравнению с другими линиями, которые можно провести через ставку без риска и остальные портфели на границе Марковца. Обозначим угловой коэффициент прямой Н через <р. Он равен отношению премии за риск рыночного портфеля к его риску:
Чтобы найти уд. веса активов в портфеле M, необходимо максимизировать значение целевой функции <р при условии, что
В функции (4.16) риск портфеля равен:
Запишем его как:
Для нахождения максимума функции (4.16) необходимо учесть ограничение.
Поскольку оно имеет вид
Также учтем, что
ИЛИ
Чтобы определить максимум функции (4.17), надо найти ее частные производные по 0, и приравнять их к нулю. Найдем производную функции <р по вк в общем виде:
Умножим (4.18) на
или
В равенстве (4.19) величина
или
или
Обозначим величины
На основе равенства (4.21) для п бумаг составляем систему из п уравнений с п неизвестными:
Решив данную систему уравнений получим значения z;. Согласно определению значений zt они пропорциональны величинам #;. Коэффициент пропорциональности - это Я. Поэтому определить уд. веса активов в рыночном портфеле можно из отношения:
Поясним представленный алгоритм определения рыночного портфеля на примере для трех бумаг. Пример 1. Пусть все множество рискованных активов представлено только тремя бумагами. Стандартное отклонение доходности первой (в десятичных значениях) равно 0,2, второй - 0,3 , третьей - 0,4. Ковариация доходностей первой и второй бумаг составляет 0,048, первой и третьей - 0,056, второй и третьей - 0,108. Ожидаемая доходность первой бумаги равна 12%, второй - 16%, третьей - 22%, ставка без риска - 5%. Определить уд. веса бумаг в рыночном портфеле. Решение. Запишем систему уравнений (4.22):
или
Решая систему (4.23) получаем:
Таким образом, первую и третью бумаги следует купить в уд. весах 66,67% и 92,98%, а вторую продать в уд. весе 59,64%. Ожидаемая доходность и риск рыночного портфеля составят: |
||||||||||||
|
|
||||||||||||










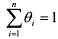 . Решим данную задачу для случая, когда короткие продажи разрешены.
. Решим данную задачу для случая, когда короткие продажи разрешены.
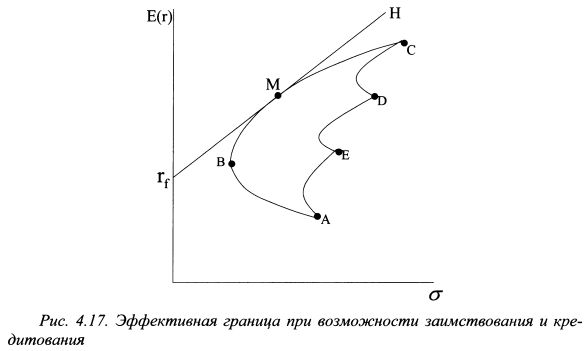
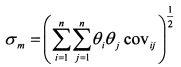
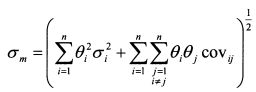
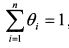 , то включим его непосредственно в числитель уравнения (4.16) следующим образом:
, то включим его непосредственно в числитель уравнения (4.16) следующим образом:
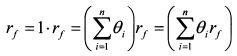
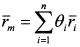 . Функция (4.16) принимает вид:
. Функция (4.16) принимает вид:
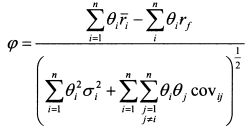
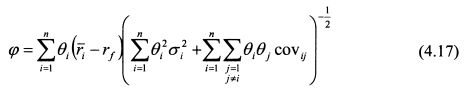
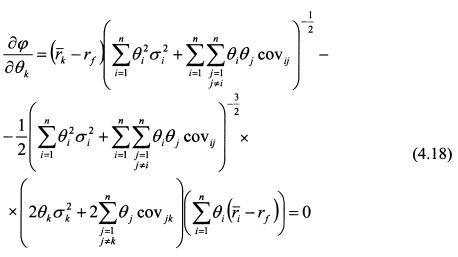
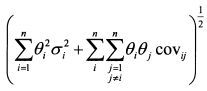 и преобразуем:
и преобразуем:
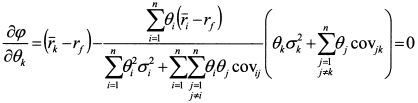
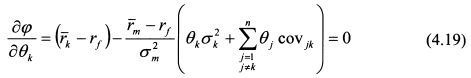
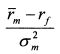 является константой, поскольку это премия за риск рыночного портфеля, деленная на его риск, измеренный дисперсией. Обозначим ее через Л. Тогда:
является константой, поскольку это премия за риск рыночного портфеля, деленная на его риск, измеренный дисперсией. Обозначим ее через Л. Тогда:
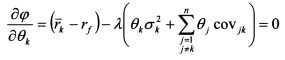
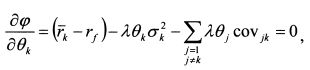
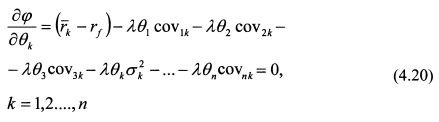
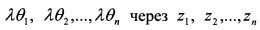 . Тогда (4.20) запишется как:
. Тогда (4.20) запишется как: