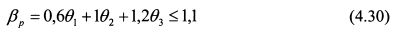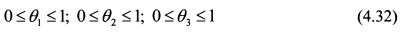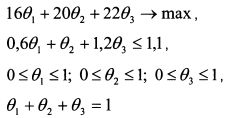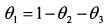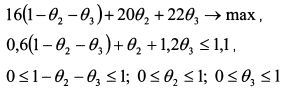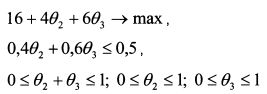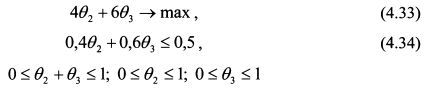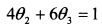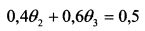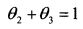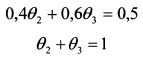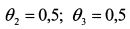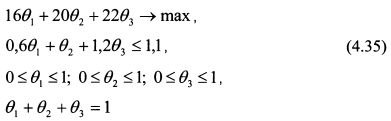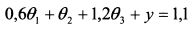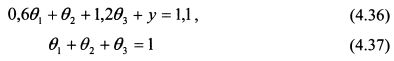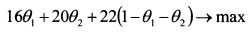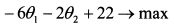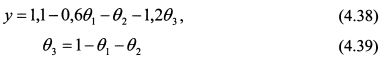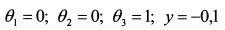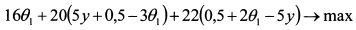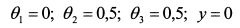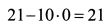4.7. Определение оптимального портфеля с помощью линейного программирования

Задача линейного программирования возникает при линейности целевой функции и ограничений. Линейное программирование можно использовать для определения оптимального портфеля, если задать риск активов и портфеля коэффициентами бета и поставить задачу максимизировать доходность портфеля при данном уровне риска. В этом случае как целевая функция, так и ограничения линейны. Рассмотрим использование метода линейного программирования на примере формирования оптимального портфеля из трех акций.

Пример 1.

Ожидаемая доходность первой бумаги равна 16%, второй - 20%, третьей -22%. Бета первой бумаги составляет 0,6, второй - 1, третьей - 1,2. Определить уд. веса бумаг в портфеле, чтобы его ожидаемая доходность была максимальной и бета не превышала 1,1. Веса бумаг в портфеле могут быть только неотрицательными. Заимствование средств не разрешено.

Решение.

Ожидаемая доходность портфеля равна:

Бета портфеля не должна превысить значение 1,1. Поэтому риск портфеля запишем как неравенство:

Сумма всех уд. весов в портфеле равна единице:

Уд. вес каждой бумаги должен быть не меньше нуля и не больше единицы:

В задаче функция (4.29) является целевой. Она подлежит максимизации. Ограничениями выступают условия (4.30)-(4.32). Таким образом, постановку задачи можно записать как:

Решим задачу графически. Чтобы представить решение на плоскости, выразим уд. вес первой бумаги из ограничения (4.31):

и подставим его в целевую функцию и другие ограничения:

или

В целевой функции присутствует константа - число 16. Она не влияет на получение оптимального решения, поскольку прибавление константы к функции не изменяет точку ее максимума. Поэтому исключим ее из целевой функции. Условия задачи запишутся как:

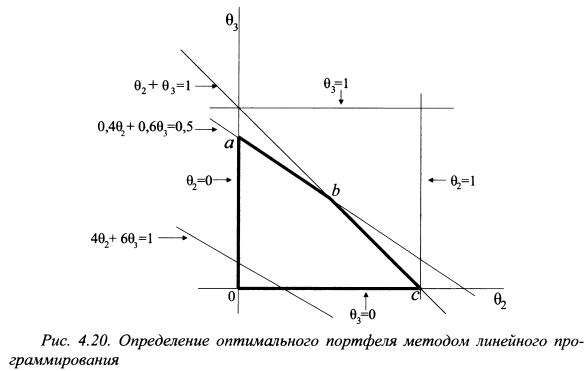
Представим на графике ограничивающие функции, записав их как равенства (см. рис. 4.20). Все возможное множество портфелей, отвечающее ограничениям задачи, расположено внутри четырехгранника abco. Теперь необходимо представить на графике линии уровня, соответствующие разным значениям доходности портфеля. Оптимальный портфель будет расположен в точке касания допустимого множества портфелей abco и линии уровня, которая расположена как можно дальше от начала координат вправо и вверх. Для иллюстрации проведем на графике одну линию уровня, соответствующую ожидаемой доходности портфеля 17%. Поскольку целевую функцию мы уменьшили на 16, то такая линия уровня имеет вид:

Если двигать ее по направлению вправо и вверх, то получим точку касания допустимого множества abco и линии уровня. Это точка b. Она показывает уд. веса второй и третьей бумаг в оптимальном портфеле. Точка b расположена на пересечении прямых

и

Поэтому уд. веса бумаг найдем решив систему уравнений:

Отсюда:

Из равенства (4.31) делаем вывод, что вх = 0.

Общий метод решения задач линейного программирования - это симплекс-метод. Он имеет итерационный характер. Определяются значения неизвестных и подставляются в целевую функцию. Если значения целевой функции можно улучшить, то вычислительные действия повторяют и находят новые значения неизвестных. Их вновь подставляют в целевую функцию. Действия повторяются до тех пор, пока не будет найдено оптимальное решение, т.е. когда уже нельзя улучшить значение целевой функции.

Пример 2.

Решим задачу в примере 1 симплекс-методом. Как и примере 1 постановка задачи имеет вид:

В симплекс-методе от условий неравенств переходят к равенствам, вводя добавочные переменные. Введем добавочную переменную у > 0 и запишем условие (4.35) как равенство:

Тогда имеются два ограничивающие равенства:

Все переменные делят на базисные и свободные. Базисные переменные выражают через свободные. Количество свободных переменных равно разности между общим числом переменных и числом ограничивающих уравнений. Общее число переменных в задаче равно четырем - 0,, 02, 03, у, - а ограничивающих уравнений два. Поэтому получаем две свободные и две базисные переменные. Выберем в качестве базисных переменных 03 и у. Тогда свободными переменными будут 0, и 02.

Из целевой функции необходимо исключить базисные переменные, выразив их через свободные. Тогда:

или

Выразим базисные переменные через свободные:

или, подставив значение 03 из (4.39) в (4.38):

На каждом шаге поиска решения значения свободных переменных принимают равными нулю и определяют значения базисных переменных. Поэтому положим значения свободных переменных равными нулю: вх = 0; 02 = 0 Тогда из равенств (4.40) и (4.41): у = -0,1; 03 =1. Таким образом, получаем первое возможное решение:

Однако данное решение является недопустимым, так как величина у получилась отрицательной, что противоречит введенному условию ее не отрицательности. Следовательно, ее необходимо перевести в разряд свободных переменных, взяв вместо нее новую базисную переменную: вх или в2. Какую из них следует перевести в разряд свободных? В равенстве (4.40) большую угрозу для получения отрицательности величины у представляет #2, поскольку ее коэффициент меньше чем у вх. Это значит, что, при текущем значении вх = 0 при увеличении значения в2 величина у будет с меньшей скоростью уходить от отрицательности, чем в случае увеличения вх приняв в2=0. Поэтому новой свободной переменной делаем в2. Выражаем новые базисные переменные из равенств (4.40) и (4.41) через свободные:

или, подставив (4.42) в (4.43):

Исключаем из целевой функции базисные переменные, выразив их через свободные:

или

Положим значение свободных переменных равными нулю. Из (4.44) и (4.45) получаем решение:

При этих значениях переменных значение целевой функции равно:

В максимизируемой функции (4.46) нет переменных с положительным знаком. Следовательно, решение нельзя улучшить. Поэтому, для получения максимальной доходности портфеля при введенных ограничениях необходимо купить только вторую и третью бумаги в равных уд. весах. При этом ожидаемая доходность портфеля составит 21%.

Содержание

Далее