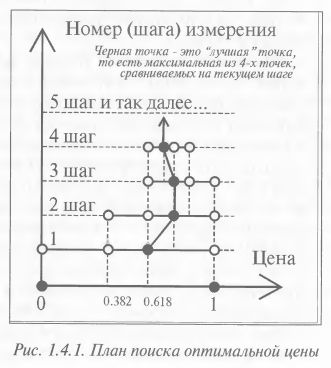
1.4. Быстрый поиск лучшей цены – Фибо-поиск

Приступаем, господа, к обоснованию права на жизнь нашей веры, которую мы предлагаем принять и вам.

Наша вера состоит в том, что применимость Фибо-соотношений для поиска лучшей цены на товарном рынке – это не следствие разумности космоса, и даже не результат того, что мужчины находятся под влиянием планет и женщин, у которых высота пупка находится на уровне 0.618 от их роста. Существование Фибо-пропорций – это следствие того, что товарный рынок – сверх-рациональная среда, стремящаяся получить самым коротким путем максимальную прибыль.

Теорема Воробьева Н.Н. о поиске максимального значения функции кратчайшим путем

В 50-х годах господин Воробьев Н.Н., известный советский математик и профессор МГУ, поставил и решил задачу о том, каким образом для некоторой функции F кратчайшим путем (то есть, с минимальным количеством измерений) и допуская при этом максимальную ошибку найти такой ее параметр X, чтобы значение F, соответствующее этому X, с заданной точностью Q было ее максимальным значением. Иными словами, нужно с минимальным количеством измерений и с точностью Q найти максимальное F, допуская при этом максимальную ошибку.

Задачу поиска осложняет то обстоятельство, что мы практически ничего не знаем о реальных значениях функции в тех точках, где измерения еще не были произведены. Да уж, тяжелые условия работы. Неопределенность полная. Ну да ладно, разберемся...

Таким образом, в нашем распоряжении последовательно могут появляться только те значения F и в тех точках X, где мы реально произвели измерения.

Вышеописанное ограничение – «найти искомую точку путем минимального количества измерений при условии того, что каждый раз необходимо совершать максимальную ошибку» – называется условием «минимакса». А полный алгоритм или, по-другому говоря, план работы, который должен быть найден, называется «оптимальным планом поиска».

Да, кстати, единственное, что по условию теоремы было известно об этой функции F, – это то, что на протяжении всей области изменения ее параметра X где-то в неизвестной пока что нам точке X' существует один-единственный максимум Fmax. И еще две коротких «вводных», которые были включены в условия задачи: во-первых, для начала поиска максимального F был выбран некий диапазон от X1 до Х2, а во-вторых, функция F должна быть, попросту говоря, плавно изменяющейся, гладкой и монотонной, то есть без перегибов.

Давайте подумаем, как же, с точки зрения homo sapience, то есть человека разумного, может быть произведен поиск?

В связи с тем, что мы ничего не знаем о значениях функции до тех пор, пока их не измерили, мы, естественно, просто будем вынуждены последовательно брать все новые и новые значения X и для них проводить измерения функции F. Как только появляется некое новое значение F, нам придется сравнивать его с ранее подсчитанными значениями функции. Затем, найдя, что какое-то из них лучше удовлетворяет требованиям, будем сравнивать его уже с тем новым, которое будет посчитано позже...

Если набраться терпения и, не имея представления о решении теоремы Воробьева, действовать по такому алгоритму в лоб, то процесс поиска может продолжаться ну очень долго. И даже ваша готовность прекратить поиск в тот момент, когда значения X и F будут если не самые лучшие, то уж хотя бы в высокой степени близки к лучшим, поможет слабо. Причина в том, что на любом отрезке число точек бесконечно, а вы, скорее всего, выбираете точки для новых измерений далеко не самым оптимальным образом.

Где же выход? В чем же состоит оптимальный план поиска?

Пропуская длинное математическое обоснование, сразу даем вам ответ, найденный нашим соотечественником, господином Воробьевым Н.Н.. Иллюстрация к нему – на рисунке 1.4.1.

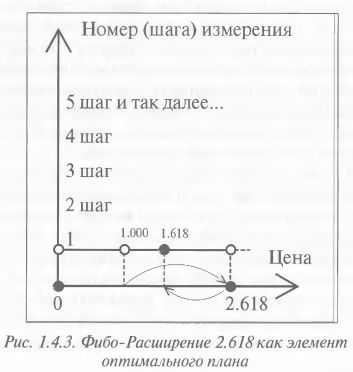
Оптимальный план поиска максимального значения функции F на отрезке длиной L (скажем, от 0 до 1) оказывается такой:

• Сначала необходимо решить, с какой точностью Q мы хотим найти аргумент X, соответствующий Хmax. Хmax – это значение X, при котором F=Fmax. To есть, необходимо задать Q – такой интервал абсолютной погрешности параметра X по сравнению с Хmax, при попадании в который мы прекращаем поиск.

• Теперь переходим к основным действиям и делим текущий тестируемый отрезок «0-1» на три части двумя внутренними точками, отстоящими от его левого края «0» на расстояния 0.382 и 0.618.

• Затем сравниваем значения F для точек 0.382 и 0.618 – на одной из них F будет больше, чем на другой; точку с большим F назовем «лучшей».

• Когда найдена «лучшая» точка, к рассмотрению принимаем такие два целых соседних отрезка, один из которых находится справа от «лучшей» точки, а другой – слева. Суммарный отрезок, состоящий из двух данных, делим еще одной точкой в пропорции 0.382; новую точку деления отложим от того края суммарного отрезка, который находится дальше от «лучшей точки».

• Теперь внутри суммарного отрезка у нас снова две точки – одна старая, которая разделяла два отдельных (была «лучшей»), и новая, которую мы построили только что. Эти две точки, как оказывается, делят суммарный отрезок тоже в пропорциях 0.382 и 0.618!

• Теперь переходим ко второму шагу – сравниваем две новые точки деления, ищем лучшую точку, выбираем два отрезка вокруг нее, делим еще одной и вновь переходим ко второму шагу... и так далее.

• В итоге, после какого-то измерения с номером N будет найдена такая точка X, которая попадет в интервал от (Xmax-Q) до (Xmax+Q), где Хmax – аргумент, соответствующий абсолютному Fmax, a Q – абсолютная погрешность, которую мы считаем приемлемой.

Понятно, господа, что таким способом найти абсолютное максимальное значение функции Fmax нереально, потому что на любой линии бесконечное множество точек, то есть к максимуму можно приближаться бесконечно. Но все же, если строго придерживаться данного плана поиска, то он гораздо быстрее, чем любой другой способ поиска, приведет вас к нахождению искомого интервала параметра X, внутри которого с заданной степенью точности Q и находится единственная точка Хmax, которой, в свою очередь, и соответствует самое что ни на есть максимальное значение функции Fmax.

Итак, Воробьев Н.Н. предложил оптимальный план поиска максимального значения функции F на заданном отрезке, – и выше этот план вам описан. Воробьев назвал его «Фибо-планом». И именно коэффициенты Фибоначчи (0.382 и 0.618) играют в этом плане ведущую роль. В будущем вы увидите, что эти числа соответствуют величине Коррекций, являющихся обязательными спутниками импульсных движений. Но это еще не все!

Л.В. Братухин, автор идеи моделирования поведения биржевой толпы условием «минимакса», сформулировал ряд интересных следствий из теоремы Воробьева. Ниже мы их перечисляем.

Во-первых, если в процессе оптимального Фибо-поиска обнаруживается, что в заданном интервале (для простоты – в интервале от 0 до 1) не существует точки, где функция оказывается максимальной, то изучаемый интервал можно расширить.

Во-вторых, Расширение должно быть сделано не абы как, а таким образом, чтобы расширенный интервал был связан с первоначальным интервалом пропорциями 0.618, 1.618. Выражаясь математическим языком, расширенный отрезок должен быть «фибо-сопряжен» с внутренними, то есть, внутренние отрезки должны быть длиной 0.382 или 0.618 от нового расширенного. Иллюстрация – на рисунке 1.4.2.

В-третьих, алгоритм Фибо-поиска останется оптимальным, если уже протестированный отрезок расширить в Фибо-пропорции, большей, чем 1.618, – то есть, в соотношении 2.618. Дело в том, что когда мы для вновь полученного «2.618-расширенного» отрезка будем проводить работу по оптимальному плану поиска, то уже при ближайшем делении расширенного отрезка однозначно попадем в точку 1.618 – она обязательно будет протестирована! Смотрите рисунок 1.4.3.

Таким образом, выводы самого господина Воробьева и полученные из его теоремы господином Братухиным следствия показывают, что внутренние Фибо-соотношения и внешние Фибо-Расширения – равноправные участники процесса поиска максимального значения функции. А тот факт, что Расширения помогают оптимальным образом выйти за рамки первоначально заданного интервала, делает Фибо-план эффективнейшим инструментом для поиска ответов на два чрезвычайно важных вопроса:

• как найти максимум функции (аплодируют математики с физиками!);
• и как найти тот максимальный уровень, куда, возможно, придет цена (ваши аплодисменты, господа!).

После бурных аплодисментов мы дадим небольшой комментарий.

Спрос – это не просто объем покупок, которые могут совершить все ваши потенциальные покупатели. Спрос – это математическая функция, отражающая количество товара, которое может быть продано при данной цене. При условии умеренности интервала, в котором колеблются цены, график спроса можно представить в виде прямой линии. Доход от продажи партии товара при данном спросе подсчитывается путем перемножения текущей величины спроса (количества товара) на текущую цену. И при неизменных внешних условиях график дохода является как раз той самой функцией с единственным максимумом! Иными словами, только в одной точке торговец продает такое количество товара и по такой цене, что его доход оказывается максимальным!

Что же это значит? Это значит, что для поиска оптимальной цены при неизменных внешних условиях одиночный торговец может пользоваться описанным выше Фибо-планом – ведь ему нужно решить «обычную» математическую задачу! – и если он воспользуется Фибо-соотношениями, то такой способ поиска будет самым эффективным!

Таким образом, мы смогли смоделировать поведение Рынка, как если бы он был сверх-рациональной средой, стремящейся к максимуму прибыли. А так как Рынок и есть эта самая сверх-рациональная среда, которая не сделает шагу, если впереди не увидит хороших заработков, то можно предположить, что наша модель оптимального Фибо-поиска обосновывает применимость и рациональность уровней Фибоначчи. Таким образом, считаем доказанным тот факт, что Фибо-соотношения как инструмент работы не навязаны нам космосом «от балды» и не являются элементами молитвы. Их рациональное использование не связано с эстетичностью прекрасных женских форм. Фибо-соотношения – элемент наиболее рационального поведения самого торговца в процессе его работы над достижением собственной цели – заработать как можно больше денег. А торговец – это все Рыночное Предложение, состоящее из миллионов мельчайших частиц – замыслов и стремлений отдельных трейдеров. Отсюда и максимальная ошибка при поиске оптимальной цены.

Конечно, остался неясен еще один момент: откуда же сам Рынок (то есть, толпа продающих свой товар трейдеров) знает о рациональности использования пропорций Фибоначчи, если сами отдельно взятые трейдеры знают о них лишь на уровне легенд, пусть даже и используют в работе?

Вот здесь, господа, уже можно найти место объяснениям, опирающимся на существование неких «математическо-психологическо-биологических часов» в мозге человека, отмеряющих в подсознании некий объективный ритм, в котором (желательно!) чтобы все мы и работали. Например, по мнению одного из авторов курса, А.С. Кияницы, глобальная жизнеспособность уровней Фибоначчи может быть объяснена «мягкой дискретностью» мышления человека, которое, в свою очередь, объясняется теми самыми биологическими свойствами мозга. Что же понимается под «мягкой дискретностью»?

Предположим, на графике обозначилось некое завершенное Движение цены, а после него начало развиваться новое. Более раннее Движение цены в момент его возникновения стало для мозга «привычным» делом и было принято за «стандарт». И все, что теперь не укладывается в стандарт, вызывает биологическую реакцию. «Мозолит глаза», так сказать. Пока цена далека от уровней, мы работаем активно, но спокойно – совершаем сделки, покупаем, продаем и, в целом, не сильно беспокоимся о будущем. Мы наивно считаем, что мы принимаем решения и управляем миром. Но в те моменты, когда отношение нового хода к старому становится особенно близко к какой-либо из Фибо-пропорций, активность мозга повышается особенно сильно – и не потому, что мы сами этого хотим или считаем это рациональным, а потому, что хотим мы этого по приказу Природы. И вот в такие моменты процессы мышления ускоряются, человек начинает строить пока еще несуществующие «сценарии», волноваться и терять терпение, каким бы хладнокровным он ни был. И в итоге, на уровнях цен, соответствующих Фибо-пропорциям, и в связи с состоянием толпы, цена совершает прыжки в сторону какого-либо из соседних уровней. «Выпрыгнув» с текущего Фибо-уровня, мы, люди, опять успокаиваемся, пока с нами не повторится то же самое, но на другой позиции. Так Природа управляет нами, чтобы Рынок в лице толпы трейдеров, состоящей из отдельных нас, мог рационально и в соответствие с Фибо-планом управлять ценой. Вселенная стремится к четкой организации всех своих процессов.

Все, что сказано выше об отдельных людях, очевидно, должно распространяться и на трейдеров, целенаправленно эксплуатирующих Фибо-пропорции. Но между «последователями Фибоначчи» и «обычными» людьми есть разница. Разница в том, что «последователи» умеют эксплуатировать Фибо-пропорции, в то время как у «обычных» людей эти пропорции лишь вызывают природные эмоции.

Поскольку люди – существа недисциплинированные или стремящиеся найти собственную истину, или просто жаждущие считать себя независимыми и свободными от всех и вся, то большинство отдельно взятых людей делает ошибки, поступая отнюдь не строго «по Закону Рынка». Их ошибки превращаются в «слитые депозиты» или удачно пополняют их же банковские счета. Но один человек или даже тысяча людей не меняют общей ситуации – Рынок по-прежнему обращается к пропорциям Фибоначчи, ведя Фибо-поиск оптимальной цены.

Вот так, господа, можно объяснить, откуда вообще на финансовых рынках взялись уровни – есть мы и наши интересы, есть Рынок как часть Природы и есть его рациональные интересы, есть Природа, которая является «куратором» Рынка, есть наша модель, которая объясняет поведение Рынка.

Если же задаться вопросом о том, кто «настроил» саму Природу на Фибо-волну, то задача исследователей будет уже иная – не объяснить смысл пропорций или их рациональность, не убедить нас в том, что использование Фибо-соотношений приносит деньги, а найти первопричину всего сущего. Но это уже слишком сложный вопрос, чтобы обсуждать его здесь. Отложим до лучших времен. Займемся пока что валютным дилингом.

Содержание

Далее