Значение метода оценки

Любой метод поиска должен иметь некоторый способ определения того, является ли торговая модель «хорошей», чтобы принять ее или отвергнуть. Хорошей торговой моделью может быть модель с максимальной прибылью, с максимальной прибылью на сделку, с максимальным процентом выигрышей или с комбинацией трех этих показателей. Такой метод определения качества торговой модели называется методом оценки. В статистике он также известен как целевая функция. Хорошая торговая модель зависит отнюдь не только от чистой прибыли. На самом деле, хорошая модель – это комплекс показателей.

При использовании методов поиска очень важным оказывается тип оценивания. Поскольку методы поиска, по определению, в процессе поиска лучшего пути постоянно принимают торговые модели или отвергают их, крайне важно применять правильный метод оценивания: именно этот метод обладает наибольшей предсказательной силой и будет успешным в реальном трейдинге. При использовании неправильного или неподходящего типа оценивания можно пропустить хорошую модель; что еще хуже, можно выбрать для торговли в реальном времени плохую модель.

При выборе типа оценки лучше всего руководствоваться принципом – «Будь внимателен, когда что-то просишь, потому что можешь это получить». Например, если критерием отбора является максимальная чистая прибыль, то будет отобрана модель, приносящая максимальную прибыль. В конечном счете, для трейдера важна именно прибыль. Тогда почему такая модель может быть плохой? Потому что одна лишь максимальная прибыль не является адекватным показателем качества торговой модели. Например, 60% этой максимальной чистой прибыли могли быть получены моделью на одной крупной сделке, которая (будем надеяться) может никогда больше не повториться, такой как короткая продажа во время Краха фондового рынка в октябре 1987 года. Или большая часть этой прибыли могла быть получена в первой половине тестового периода и могла маскировать катастрофические убытки во второй, более актуальной половине. Показатель одной только чистой прибыли игнорирует очень важное требование равномерности распределения прибылей.

Более того, поиск наибольшей чистой прибыли полностью игнорирует вопрос риска. Стратегия с максимальной чистой прибылью может также иметь очень большое и неприемлемое проседание счета. Другой ее недостаток в том, что лучшая прибыль могла быть получена посредством очень небольшого числа сделок. Модель с таким набором сделок имеет ограниченную статистическую валидность.

Метод оценки исключительно по чистой прибыли игнорирует многие важные характеристики, которые необходимо учитывать при выборе топ-модели, обладающей наибольшей предсказательной способностью в отношении будущей реальной прибыли. Подчеркнем некоторые из ключевых характеристик настоящей топ-модели:

• Равномерное распределение сделок.
• Равномерное распределение прибыли.
• Приемлемый риск.
• Статистическая валидность.

Тип оценки должен быть разработан для отбора наиболее устойчивой и стабильной торговой модели, которая не обязательно будет самой прибыльной. Мы выбрали в качестве типа оценивания чистую прибыль, чтобы осветить некоторые факторы, влияющие на устойчивость модели.

Неправильный тип оценки может фактически и неумышленно привести в процессе оптимизации к подстройке. Метод оценивания, отбирающий модели не по их устойчивости, ставит под сомнение весь процесс тестирования. При реальном трейдинге устойчивая торговая модель, скорее всего, принесет прибыль, а неустойчивая модель – убытки.

Выбор критериев оценки

В этом разделе приводятся различные критерии оценки, распространенные в большей или меньшей степени, а также краткие описания их сильных и слабых сторон.

Чистые прибыли и убытки – чистый выигрыш или проигрыш модели в долларах или каких-то других денежных единицах. Хотя трейдер стремится к максимально возможной прибыли, чистая прибыль, как единственный показатель – ненадежный метод оценки. На нее могут чрезмерно влиять отдельный крупный выигрыш или проигрыш. Она полностью игнорирует число и распределение сделок. Безусловно, чистая прибыль – важный элемент, и она может использоваться в качестве критерия допустимого минимума доходности. Например, учитывая проскальзывание и другие издержки, доходность $100 на сделку может считаться минимально приемлемым показателем.

Норма доходности – альтернативный способ выражения чистых прибылей и убытков и полезная мера эффективности модели, поскольку она облегчает сравнение различных временных периодов и разных инструментов. Однако в качестве метода оценивания она подвергается той же критике, что и чистая прибыль. Она полезна для установки минимальной цели, но неприемлема в качестве единственного показателя.

Максимальное проседание счета – показатель риска и важный показатель эффективности модели. Оно оценивается двумя способами: как долларовая величина крупнейшей последовательности Убыточных сделок, или как наибольшее проседание кривой доходности. В любом случае оно представляет «защитный» критерий, поскольку ищет наименьший долларовый проигрыш, а не наибольший долларовый выигрыш. В качестве критерия оценки максимальное проседание обладает теми же слабыми сторонами, что и чистая прибыль, и поэтому неприемлемо в качестве единственного показателя. Максимальное проседание полезно в качестве порогового ограничения. Модели, превышающие определенное проседание, могут сразу исключаться из рассмотрения. Однако минимальное проседание является недостаточным в качестве единственного критерия: проседание равно нулю тогда, когда у модели нет проигрышных сделок, и, вероятнее всего, выигрышных тоже.

Корреляция между кривой доходности и идеальной прибылью (perfect profit) – критерий оценки, неявно включающий распределение сделок. Более важно то, что этот показатель рассчитывает коэффициент полезного действия модели на основе реальных прибыльных возможностей, предоставляемых рынком.

Идеальная прибыль – это теоретический показатель рыночного потенциала, а именно, общая долларовая прибыль, получаемая в результате покупки каждой «впадины» и продажи каждого «пика», возникающих в ценовом движении. Очевидно, что данная задача невыполнима, откуда и название – идеальная прибыль. Математически она равна сумме разностей цен, взятых по модулю.

Кривая доходности модели – это накопленная стоимость всех совершенных сделок. Кривая доходности связана с идеальной прибылью стандартным статистическим показателем – коэффициентом корреляции, который находится в интервале между -1 и + 1. Значение -1 будет плохим, поскольку оно показывает, что при повышении идеальной прибыли размер счета снижается. Значение +1 является хорошим, так как свидетельствует о том, что по мере роста идеальной прибыли размер счета тоже растет. Формула коэффициента корреляции между идеальной прибылью и кривой собственности следующая:

Чем корреляция между кривой доходности торговой модели и идеальной прибылью выше, то есть, ближе к +1, тем более эффективно модель использует рыночные возможности. Почему? Идеальная прибыль представляет собой куммулятивный показатель, а поэтому будет расти на протяжении всего торгового периода. Хорошая торговая модель будет также демонстрировать устойчивый рост кривой доходности. Если рынок становится спокойным, для роста идеальной прибыли будет характерна тенденция к повышению с меньшей скоростью. Лучшая модель также будет демонстрировать некоторую стабилизацию или медленный рост, вместо понижения кривой доходности в течение такого периода. Аналогично, когда рыночная волатильность находится на пиковом уровне, это будет отражено резким ростом идеальной прибыли. Лучшая модель будет также демонстрировать сильный рост прибыли, заметный по увеличению угла наклона кривой доходности.

В отличие от чистой прибыли, данный показатель будет отдавать предпочтение торговым моделям, дающим устойчивую прибыль с тем же темпом, с каким растет идеальная прибыль, и не несущим крупных убытков, когда рост идеальной прибыли замедляется. Это отличный кандидат на роль единственного критерия. Это также хороший кандидат на роль порогового ограничения.

Пессимистическая доходность на маржу (The pessimistic return on margin, PROM) – это годовой доход на маржу, скорректированный на «пессимистическое допущение», согласно которому в реальной торговле система будет выигрывать меньше и проигрывать больше, чем при тестировании.

PROM корректирует валовую прибыль путем вычисления новой, пессимистической, заниженной валовой прибыли. Первый шаг – найти число выигрышных сделок, уменьшенное на квадратный корень или скорректированное на свою стандартную ошибку. Это скорректированное число выигрышных сделок далее умножается на среднюю выигрышную сделку, чтобы получить новую, заниженную валовую прибыль.

Затем PROM корректирует валовой убыток путем вычисления нового, пессимистического, завышенного валового Убытка. Первый шаг – вычисляется количество проигрышных сделок, увеличенное на квадратный корень из себя или скорректированное на свою стандартную ошибку. Затем это скорректированное число проигрышных сделок умножается на среднюю проигрышную сделку, чтобы получить новый, завышенный валовой убыток. Далее новые чистые прибыль и убыток вычисляются по этим скорректированным валовым прибыли и убытку. Это, в свою очередь, делается для получения годовой нормы доходности на маржу. Формула следующая:

Допустим, годовая валовая прибыль составляет $25,000, годовой валовой убыток – $10,000, и маржа $10,000. В соответствии со стандартными вычислениями, годовой доход на маржу составит 150% ([$25,000-$10,000)]/$10,000=1.5х100=150%). PROM даст заниженную оценку:

На этом примере ясно показано, почему данный показатель называется пессимистическим. Он исходит из предположения, что торговая система не будет выигрывать в реальном времени так часто, как при тестировании, а нести убытки в реальном времени будет чаще, чем при тестировании. PROM отражает эти пессимистические допущения посредством корректировки чистой прибыли на стандартную ошибку. А раз так, он является более консервативным показателем. Его ценность также в том, что он включает число выигрышей и проигрышей.

PROM является достоверной мерой эффективности модели, поскольку учитывает валовую прибыль, средний выигрыш, валовой убыток, средний проигрыш, число выигрышей и число проигрышей. Как следует из его названия, PROM пессимистически взвешивает прибыль (путем ее уменьшения) и убыток (путем его увеличения).

Пессимистическая доходность на маржу – очень хороший и достоверный показатель эффективности торговой модели. Будучи «пессимистически» скорректированной, доходность на маржу также представляет хороший способ сравнения эффективностей различных торговых моделей.

Существует две более строгих производных от PROM – PROM минус максимальный выигрыш и PROM минус максимальная выигрышная серия. Как следует из их названий, эти показатели корректируют валовую прибыль еще в большей степени, чем PROM. PROM минус максимальный выигрыш устраняет из валовой прибыли максимальную единичную прибыль, а затем вычисляет PROM. Это более строгий показатель, чем PROM. Его самое большое достоинство в том, что он позволяет оценить торговую систему, устранив влияние максимальной выигрышной сделки, которая могла быть вызвана ценовым шоком. Там, где исключительно крупного выигрыша не было, этот показатель очень близок к PROM. Однако там, где крупный выигрыш был получен за счет Краха фондового рынка 1987 года, PROM минус максимальный выигрыш дает меру эффективности модели, исключающую такую непредсказуемую прибыль.

PROM минус максимальная выигрышная серия устраняет из валовой прибыли наибольшую последовательность прибылей, а затем вычисляет PROM. Это наиболее строгий показатель. Он обеспечивает меру эффективности торговой модели, скорректированную на исключительную выигрышную серию, которая могла быть вызвана необычайно благоприятными торговыми условиями. В поиске наиболее устойчивой и стабильной торговой модели всегда лучше готовиться к худшему и надеяться на лучшее. Модель, обеспечивающая лучшую годовую доходность, и при пессимистической корректировке, и без своих лучших результатов, с большой вероятностью будет устойчивой в реальном времени.

Комплексная оценка

Комбинация различных критериев оценки предпочтительней, чем отдельный показатель. При этом конкретные пороговые ограничения эффективности, вносящие вклад в устойчивость модели, устанавливать легче. Например, ранжируйте топ-модели с помощью PROM и устанавливайте следующие критерии:

• чистая доходность больше $5,000
• максимальное проседание меньше $5,000
• минимум сделок за год – 10.

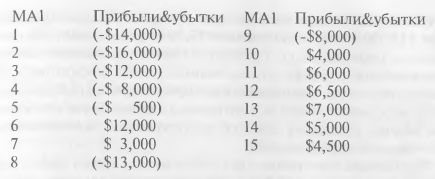
Ранжирование топ-моделей с помощью достоверного показателя, такой как PROM, устранит возможные проблемы. Исключение моделей, приносящих менее $5,000 или имеющих проигрышную серию более $5,000, устанавливает определенный минимальный критерий эффективности. Исключение моделей, торгующих менее 10 раз в год, должно обеспечить адекватный размер выборки. Ранжирование с помощью PROM моделей, удовлетворяющих этим минимальным критериям, будет давать наиболее устойчивые результаты.

Оценка использующая группу моделей

Всплески эффективности, или изолированные прибыли, являются проклятием оптимизации. Всплеск (выброс) эффективности представляет собой статистическую аномалию. Рассмотрим крайний случай на примере торговой модели, основанной на двух скользящих средних. Оптимизация одной скользящей средней дает следующие результаты:

Топ-модель в этом примере – это модель, использующая 6-дневную скользящую среднюю и приносящая прибыль $12,500. В изолированном виде модель выглядит неплохо. Но при рассмотрении в контексте все выглядит иначе. Один шаг в сторону любого из соседних тестов, 5-дневной или 7-дневной скользящей средней, показывает резкое падение эффективности до убытка ($500) и небольшой прибыли ($3,000), соответственно. При двух шагах в любую сторону эффективность катастрофически падает до убытков ($8,000) и ($13,000).

Есть и другой пик эффективности – при 13-дневной скользящей средней, дающей прибыль $7,000. Это намного меньше предыдущего пика $12,500. Однако с учетом окружающих тестовых результатов этот пик выглядит более привлекательно. Один шаг в любую сторону приводит к прибылям $6,500 и $5,500, соответственно. Два шага дают прибыли $6,000 и $4,500, соответственно. Этот пик с каждой стороны окружен прибылями, сопоставимыми с пиковой эффективностью. Следовательно, этот второй пик скорее всего будет более устойчивой моделью, чем первый пик.

Здесь важно отметить, что 1-дневный шаг для скользящей средней с небольшим периодом не равнозначен 1-дневному шагу при большом периоде. Например, период 5-дневной скользящей средней примерно на 17% меньше периода 6-дневной средней. Период 7-дневной скользящей средней примерно на 17% больше периода 6-дневной средней. Однако в случае 13-дневной средней первый 17-процентный шаг вниз приводит к 11-дневной средней, а 17-процентный шаг вверх – к 15-дневной средней. Важно понимать это различие между шагами, выраженными в процентах и в абсолютных числовых значениях, особенно, когда предстоит сканировать диапазоны, представленные большими числами.

Некоторые методы оценки будут выбирать модель, приносящую $12,500, вместо приносящей $7,000 (при условии, что оценивание происходит по прибыли). Однако существует метод, уменьшающий эффект изолированных пиков эффективности, посредством усреднения модели по двум ее ближайшим соседям. Затем усредненная модель оценивается заново. Такое сглаживание обычно сокращает влияние изолированных, а следовательно – неустойчивых, моделей.

Рассмотрим усреднение двух обсуждаемых пиков эффективности. Первый пик $12,500 имеет ближайших соседей -$500 и $3,000. После усреднения получаем нового кандидата, $5,000, вычисляемого следующим образом:

($12,500-$500+$3,000)/3=$5,000

Второй пик $7,000 имеет ближайших соседей $6,500 и $5,000. Усредняя, получаем нового кандидата, $6,167:

($7,000+$6,500+$5,000)/3=$6,167

Этот сглаженный кандидат предпочтительнее первого сглаженного кандидата.

Оценка тестового прогона

Высокоэффективная модель, окруженная плохими моделями, вряд ли будет устойчивой, способной приносить прибыль в реальном времени. Такая модель скорее всего будет соблазнительным статистическим нонсенсом. Мы показали, что модель, окруженная схожими соседями, оказалась лучше пика прибыли. Общую эффективность всех моделей тестовой связки следует оценивать аналогичным образом. Ниже представлены некоторые руководства.

Правила статистического тестирования свидетельствуют, что лучший 1 процент всех тестовых результатов является значимым. Далее, данный принцип свидетельствует, что 5% всех тестовых результатов будут предельно значимыми. Другими словами, если при игре в дартс в мишень бросить достаточное число дротиков, возникнет группа, имеющая высокое число очков. Оптимизация лишь с небольшим числом хороших тестов будет рассматривать эти прибыли как статистически «значимые», хотя трейдера ждет разочарование, поскольку стратегия в целом не будет прибыльной. Пример 1 показывает результаты тестового прогона с числом прибыльных результатов менее 5%:

Согласно данному принципу, если было выполнено 1000 тестов торговой системы, то по определению 10 лучших тестов являются «значимыми», а следующие 40 – «предельно значимыми». Устойчивая торговая стратегия должна показывать много прибыльных результатов после устранения 50 лучших тестов из 1000.

Чтобы иметь какие-то основания говорить о валидности системы, как минимум 20% тестов должны быть на уровне прибыльности, считающемся значимым для данного рынка и системы. Такой результат показан в Примере 2:

Конечно, чем больше процент высокоприбыльных результатов, тем вероятнее, что данная торговая модель будет устойчивой. Пример 3 демонстрирует устойчивый тестовый результат:

Распределение эффективности

Как только тестовый прогон прошел тест на значимость, описанный в предыдущем разделе, полезно пересмотреть распределение общей тестовой эффективности. Это достигается путем вычисления средней, максимума, минимума и стандартного отклонения всех тестов. Самым желательным результатом будет большая средняя прибыль с минимальным разбросом (variation). Связка гестов с наименьшей разницей между максимумом и минимумом, а следовательно – с наименьшим стандартным отклонением, будет лучшей. Пример 4 показывает результаты простой торговой модели:

При сравнении одной оптимизации с другой, лучшей будет имеющая более высокую среднюю и меньшее стандартное отклонение. Совершенствуя торговую модель или внося в нее новые правила, а затем повторно тестируя, важно, чтобы число прибыльных тестов увеличивалось, средняя всей связки возрастала, а стандартное отклонение при этом не росло.

Пример 5 показывает результаты добавления в торговую модель, описанную в Примере 4, нового правила, которое снизило эффективность по каждой категории: проценту прибыльных моделей, средним результатам, средней прибыльной и средней убыточной модели. Основываясь на этих результатах, данное правило следует исключить.

Пример 6 демонстрирует результаты добавления в торговую модель правила, которое повысило эффективность по каждой категории: проценту прибыльных моделей, средним результатам, средней прибыльной и средней убыточной модели. На основе этих результатов данное правило следует включить в торговую модель.

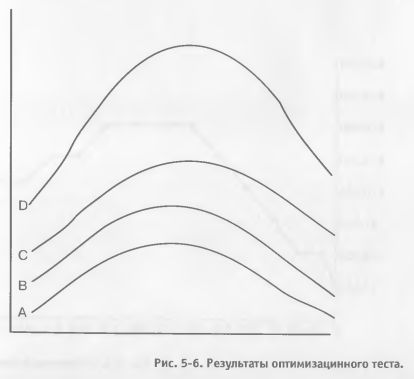
На Рисунке 5-6 линией А представлены результаты первой оптимизации. Линии В, С и D представляют различные исходы второго теста с одним усовершенствованием, внесенным в модель. Линия В отражает худший исход, потому что показывает более высокую среднюю, но гораздо большее стандартное отклонение. Линии С и D отличаются и обе лучше А, поскольку обе имеют более высокие средние и немного меньшие стандартные отклонения.

Форма тестового пространства

Несмотря на то, что форма тестового пространства кажется несколько замысловатым понятием, оно очень полезно. Тестовое пространство – это визуализация результатов тестовой связки в виде трехмерного графика. Худший из случаев, которые можно себе представить, будет напоминать горную гряду очень узких и высоких пиков прибыли. Почему это плохо? Такой модели будет не хватать устойчивости. Любой небольшой сдвиг параметра модели может изменить результаты модели с крупной прибыли на такой же крупный убыток. Такова природа неустойчивого модельного пространства. (См. Рис. 5-7)

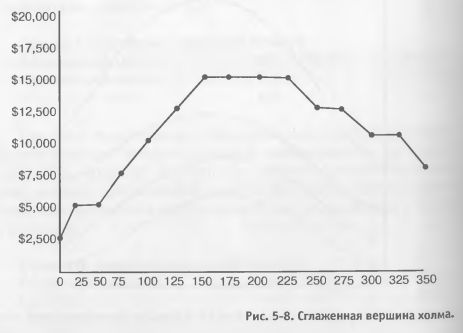
Лучшим случаем, который можно представить, будет топ-модель, расположенная на вершине большого, пологого, постепенно снижающегося холма. Этот случай хорош, потому что данная модель будет очень устойчивой. Любой небольшой или даже большой сдвиг параметра модели снизит ее эффективность на 5-10 процентов. В этом преимущество устойчивой модели. Такая модель черпает свою устойчивость из относительной нечувствительности к изменениям параметров (См. Рис.5-8).

Идеальная оптимизация по одной переменной должна создавать линию эффективности по прибыли, которая снижается постепенно в обоих направлениях от своего пика прибыли. Идеальная оптимизация по двум переменным должна создавать круг с лучшей моделью в центре и ступенчатым снижением эффективности на расходящихся концентрических окружностях. Идеальная оптимизация по трем переменным должна создавать округлый холм с лучшей моделью на вершине и ступенчатым снижением эффективности на любых концентрических окружностях большего диаметра, расходящихся от вершины этого холма.

Содержание

Далее