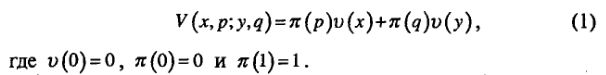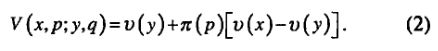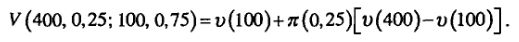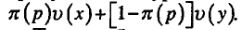|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
Теория перспективТеория перспектив Канемана и Тверски делит процесс принятия решения индивидуума на две фазы: 1) фазу редактирования [editing phase]; 2) фазу оценки [evaluation phase]. Фаза редактирования включает в себя предварительный анализ предложенной перспективы, который достаточно часто упрощает представление перспективы. Во второй фазе отредактированные перспективы оцениваются и из них выбирается перспектива, обладающая наивысшей доходностью. Рассмотрим составляющие фазы редактирования и построим формальную модель, описывающую фазу оценки. Функция фазы редактирования заключается в организации и переформулировке имеющихся возможностей для упрощения их последующих оценки и выбора. Редактирование состоит из нескольких операций, которые трансформируют исходы и вероятности рассматриваемых перспектив. Опишем основные операции фазы редактирования. • Кодирование [coding] Эмпирические исследования, с которыми мы познакомились выше, полностью подтверждают тот факт, что люди оценивают ожидаемые исходы в терминах прибылей и убытков, а! не в терминах окончательного благосостояния. Естественно, что; прибыли и убытки определяются по отношению к какой-то! нейтральной точке отсчета [neutral reference point]. За такую! точку отсчета обычно принимают текущую стоимость актива| {текущую позицию актива [current asset position]), и в этом случае прибыли и убытки совпадают с реальными объемами полученных или уплаченных средств. В то же время на местонахождение точки отсчета, а значит, и на кодирование исходов (присвоение им названия «прибыль» или «убыток») могут оказывать влияние формулировка данной перспективы и ожидания лица, принимающего решение. • Комбинирование [combination] Иногда перспективу можно упростить при помощи комбинирования вероятностей одинаковых исходов. Например, перспектива (200, 0,25; 200, 0,25) может быть сокращена до (200, 0,5) и оцениваться уже в этой форме. • Сегрегирование [segregation] Некоторые перспективы содержат в себе безрисковую компоненту, которая может быть отделена от рискованной перспективы на фазе редактирования. Например, перспектива (300, 0,8; 200, 0,2) естественным образом распадается на безрисковую прибыль (200) и рискованную перспективу (100, 0,8). Подобным образом перспектива (–400, 0,4; –100, 0,6) может быть сегрегирована на безрисковый (в смысле «наверняка») убыток в объеме 100 и перспективу (–300, 0,4). Операции кодирования, комбинирования и сегрегирования применимы только к отдельным перспективам. Следующая операция фазы редактирования может применяться к множеству, содержащему две и более перспективы. • Аннулирование [cancellation] Суть эффекта изоляции, рассмотренного нами выше, заключается в игнорировании при анализе компонентов, которые являются общими для различных перспектив. Например, в проблеме 10 наши респонденты полностью проигнорировали первый этап игры из-за того, что он оказался общим для обеих перспектив, и оценивали перспективы только на основе информации, содержащейся на втором этапе игры (см. рис. 19). Аналогичным образом они проигнорировали бонусы в проблемах 11 и 12. Помимо эффекта изоляции аннулирование включает также эффект игнорирования общих для перспектив составных частей, т. е. общих для перспектив пар исход–вероятность. Например, проблема выбора между перспективами (200, 0,2; 100, 0,5; –50, 0,3) и (200, 0,2; 150, 0,5; –100, 0,3) сводится к проблеме выбора между перспективами (100, 0,5; –50, 0,3) и (150, 0,5; -100, 0,3). К уже рассмотренным основным операциям фазы редактирования примыкают еще две. • Операция упрощения [simplification] Она заключается в упрощении перспективы при помощи округления вероятностей и значений исходов. Например, перспектива (101, 0,49), скорее всего, будет упрощена и сведена большинством людей к перспективе выиграть 100 денежных, единиц. Специальный случай операции упрощения – игнорирование индивидуумами особенно неблагоприятных исходов. • Операция определения доминанты [detection of dominance] Она заключается в просматривании предлагаемых перспектив и определении доминирующих альтернатив, которые отвергаются без какого-либо дальнейшего анализа. Применение одной из рассмотренных операций редактирования иногда может автоматически исключать возможность применения другой операции. Например, перспектива (500, 0,2; 101, 0,49) будет доминировать над перспективой (500, 0,15; 99, 0,51), если последние исходы обеих перспектив предварительно упростить до вида (100, 0,5). Таким образом, окончательный «результат редактирования перспективы» зависит от последовательности, в которой применялись операции редактирования. Фаза редактирования перспектив порождает уже знакомые нам аномалии и отклонения. Например, эффект изоляции является прямым следствием игнорирования общих компонентов перспектив. Другие аномалии в выборе индивидуумов являются следствием упрощения, которое полностью очищает перспективы от незначительных отличий. В общем случае предпочтения между перспективами не обязательно будут неизменными, ведь каждая перспектива может быть отредактирована различными операциями, причем применяемыми в различной последовательности. После фазы редактирования лицо, принимающее решение, оценивает каждую перспективу и выбирает такую, которая обладала бы наивысшей стоимостью. Общая стоимость отредактированной перспективы, которую обозначим через V, выражается в терминах двух шкал – л и и. Шкала л присваивает каждой вероятности р вес л (р), который отражает влияние вероятности р на общую стоимость перспективы. В то же время л не является вероятностной мерой и л(р)+л(1-р) обычно меньше единицы (см. ниже). Шкала v присваивает каждому исходу х число v (х), которое отражает субъективную стоимость исхода. Заметим, что исходы определяются относительно точки отсчета, в качестве которой используется нулевое значение шкалы стоимости. Таким образом, v измеряет стоимость отклонений от этой точки отсчета, т. е. прибыли и убытки. Такое представление работает с простой перспективой формы (x,p-,y,q), которая имеет, по меньшей мере, два ненулевых исхода. Владелец подобной перспективы получает прибыль х с вероятностью р, прибыль у с вероятностью q и не получает ничего с вероятностью 1 -р-q , где p + q Основное уравнение теории объясняет, каким образом комбинация величин п и v определяет общую стоимость регулярной перспективы.
Если (х, р\y,q) – регулярная перспектива (т. е. p+q< 1, или х > 0 > у, или х < 0 < у ), то тогда
Как и в традиционной теории полезности, V определена на перспективах, в то время как v определена на исходах. Две шкалы совпадают для безрисковой перспективы, где V (х,1) = V (х) = и(х).
Строго положительные и строго отрицательные перспективы оцениваются при помощи иного правила. На фазе редактирования подобные перспективы сегрегируются на две компоненты: (а) – безрисковую компоненту, т. е. минимальные прибыль или убыток, которые владелец перспективы ожидает наверняка получить или наверняка потерять; (б) – рискованную компоненту, т. е. дополнительные прибыль или убыток, который владелец перспективы ожидает получить с некоторой вероятностью. Процесс оценки подобных перспектив описывается таким образом.
Если p + q = 1 и х > у > 0 или х < у < 0, то тогда
То есть стоимость строго положительной перспективы или строго отрицательной перспективы равна стоимости безрисковой компоненты плюс разница стоимостей исходов, умноженная на вес, ассоциируемый с исходом, оказывающим наибольшее влияние на стоимость перспективы. Например:
Важным свойством уравнения (2) является то, что вес л (р) умножается на разницу v (х) – v(y), которая является рискованной компонентой перспективы, а не на v (у), которая является безрисковой компонентой перспективы. Заметим, что правую часть уравнения (2) можно преобразовать к виду
Таким образом, уравнение (2) сводится к уравнению (1), если л(р)+л(1-р) = 1. К сожалению, на практике это условие часто нарушается.
Уравнения теории перспектив сохраняют общий линейный вид, который используется в теории ожидаемой полезности. В то же время, для того чтобы в новой теории учесть известные нам отклонения, необходимо ввести предположение о том, что стоимость измеряется в терминах прибылей и убытков, а не в терминах окончательных исходов, а веса не совпадают с установленными вероятностями.
|
||||||||||||
|
|
||||||||||||