|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
8.1.4. Коэффициенты абсолютной и относительной не склонности к рискуСклонность инвестора к риску определяется выпуклостью функции полезности. Поэтому в качестве меры не склонности к риску можно взять показатели, которые бы говорили о ее выпуклости. Используют два показателя: коэффициент абсолютной не склонности к риску и относительной не склонности к риску. Коэффициент абсолютной не склонности к риску называют мерой Эрроу-Пратта (Arrow-Pratt). Для небольших значений риска он показывает величину компенсации, которую требует инвестор за принимаемый риск. Он равен:
Первая производная функции в некоторой точке определяет наклон кривой в этой точке, вторая производная - изменение наклона кривой в этой точке. Таким образом, коэффициент А представляет собой относительное изменение наклона функции полезности в каждой данной точке, т.е. изменение наклона кривой при изменении уровня богатства на небольшую величину, деленное на величину наклона кривой в этой точке. Поскольку предельная полезность инвестора не склонного к риску является величиной убывающей, то вторая производная функции полезности отрицательна. Поэтому, чтобы сделать коэффициент не склонности к риску величиной положительной, в формуле (8.9) ставим знак минус. Чем больше значение второй производной (по абсолютной величине), тем выпуклее функция. Поэтому большее значение коэффициента характеризует большую не склонность инвестора к риску. Если по мере роста богатства инвестор направляет все больше средств в рискованные активы, то он характеризуется убывающим коэффициентом абсолютной не склонности к риску. Если сумма средств, размещаемых в рискованные активы, остается неизменной, его коэффициент является постоянным. При уменьшении инвестиций в рискованные активы по мере роста богатства коэффициент является возрастающим. Между премией за риск Марковца для небольших значений риска и коэффициентом абсолютной не склонности к риску можно установить определенную зависимость. Пусть инвестор располагает богатством w0 и приобретает на него рискованный актив S (величина w0 = S), ожидаемый доход которого равен нулю. Полезность, соответствующая такой стратегии инвестора, равна:
В выражении (8.10) величину s следует понимать как случайную переменную (доход по активу), которая может принести как положительный, так и отрицательный результат к его начальному богатству w0. Таким образом, полезность является функцией текущего уровня богатства и случайной переменной, определяющей доход актива. Разложим выражение (8.10) в ряд Тейлора в окрестности точки w0 до слагаемого второй степени:
Возьмем математическое ожидание от обеих частей выражения (8.11):
ИЛИ
В правой части выражения (8.12) второе слагаемое равно нулю, поскольку нулю равен ожидаемый доход актива, т.е. E(s) = 0. В третьем слагаемом элемент E(s²) представляет собой не что иное как
Пусть гарантированной эквивалентной суммой для ожидаемого дохода рискованного актива S выступает величина (w0-z), где z можно рассматривать как сумму страховки, которую готов уплатить инвестор, чтобы исключить риск. Полезность данной суммы для инвестора равна:
Разложим выражение (8.14) в ряд Тейлора в окрестности точки w0 до первых двух слагаемых:
Величина (w0 - z) является для инвестора гарантированной эквивалентной суммой ожидаемого дохода рискованного актива S. Поэтому ожидаемая полезность владения активом и полезность гарантированной эквивалентной суммы равны, т.е.:
В результате можно приравнять выражения (8.13) и (8.15):
или
или
Представленные выше рассуждения можно рассматривать и как вывод коэффициента абсолютной не склонности к риску. Так, величина z представляет собой разность между начальным богатством инвестора w0 и уровнем богатства, соответствующим гарантированной эквивалентной сумме - обозначим ее через wc. Поэтому, z = w0 - wc. Данная величина измеряет абсолютную не склонность инвестора к риску. Чем она больше, тем менее он склонен к риску, поскольку в этом случае рискованный актив должен предложить ему более значительный ожидаемый доход по сравнению с величиной wc, чтобы он был безразличен в выборе между рискованным активом и гарантированной эквивалентной суммой. В выражении (8.16) для каждого данного рискованного актива сомножитель Коэффициент, обратный коэффициенту Эрроу-Пратта называют коэффициентом допустимости риска. Он равен:
Еще одной мерой не склонности инвестора к риску является относительный коэффициент не склонности к риску Эрроу-Пратта. Его можно рассматривать как отношение абсолютной величины не склонности к риску инвестора к его начальному богатству. Получим формулу данного коэффициента на основе рассуждений, которые были использованы применительно к выводу коэффициента абсолютной не склонности к риску. Для начального уровня богатства w0 и гарантированной эквивалентной суммы wc абсолютную не склонность к риску мы обозначили как z = w0-wc. Поэтому относительная не склонность к риску есть величина (z') равная:
т.е. это отношение абсолютной величины не склонности к риску к начальному уровню богатства. Величина z' есть не что иное как премия за риск, представленная как превышение доходности рискованного актива над ставкой без риска. Выразим из (8.17) абсолютную не склонность к риску:
Доходность, приносимая рискованным активом rs, равна:
Выразим из (8.19) доход по активу:
Выше мы записали равенство:
Подставим в него значения z и s из (8.18) и (8.20):
Разложим величину U(w0 + w0rs) в ряд Тейлора в окрестности точки w0 до слагаемого второй степени:
Возьмем математическое ожидание от этого выражения:
ИЛИ
ИЛИ
В правой части выражения (8.22) второе слагаемое равно нулю, поскольку E(s) = 0 И, следовательно E(rs)=0. В третьем слагаемом элемент Е(rs²) представляет собой не что иное как
Разложим выражение U(w0 - w0z') в ряд Тейлора в окрестности точки w0 до первых двух слагаемых:
На основе равенства (8.21) приравняем правые части выражений (8.23) и (8.24):
ИЛИ
или
В выражении (8.25) сомножитель
Коэффициент абсолютной не склонности к риску можно рассматривать как показатель, который говорит о процентном изменении предельной полезности при абсолютном изменении богатства инвестора. В свою очередь, коэффициент относительной не склонности к риску можно рассматривать как показатель, который говорит о процентном изменении предельной полезности при процентном изменении богатства инвестора. Проиллюстрируем сказанное, преобразовав формулы (8.9) и (8.26). Соответственно для коэффициентов абсолютной и относительной не склонности к риску получим результаты:
Если функция полезности характеризуется убывающей не склонностью к риску, то для нее А' < 0. Это означает, что по мере роста богатства инвестор все больше средств направляет в рискованные активы. При постоянном значении не склонности к риску А' = 0, и, следовательно, при росте богатства инвестор держит прежнее количество средств в рискованных активах. Для функции полезности с возрастающим коэффициентом не склонности к риску А' > 0, поэтому с ростом богатства инвестор уменьшает количество средств в рискованных активах. Если функция полезности характеризуется убывающей относительной не склонностью к риску, то для нее R' < 0. Следовательно, инвестор увеличивает пропорцию средств в рискованных активах по мере роста его богатства. При постоянном значении относительной не склонности к риску Д' = 0. Поэтому процент средств, инвестированных в рискованные активы, остается неизменным. Для функции полезности с возрастающим коэффициентом относительной не склонности к риску R' > 0. В этом случае процент инвестированных в рискованные активы средств уменьшается с ростом богатства. В качестве функций полезности инвестора можно выделить следующие:
Из представленных трех функций в наименьшей степени для характеристики не склонного к риску инвестора подходит квадратичная функция, поскольку оба коэффициента по мере роста богатства являются возрастающими. Это говорит о том, что инвестор с ростом богатства становится все менее склонным к риску. Такое поведение не совсем соответствует действительности, поскольку по мере роста богатства инвестор не склонный к риску готов все больше инвестировать средства в рискованные активы. Кроме того, как видно из рис. 8.7, график квадратичной функции вначале возрастает до максимального значения полезности для богатства на уровне wm и после этого убывает. Точку wm можно найти следующим образом. Выше мы определили, что первая производная функции полезности по богатству равна:
Чтобы найти максимум функции, приравняем ее к нулю:
Отсюда:
Таким образом, при росте богатства инвестора свыше уровня |
||||||||||||
|
|
||||||||||||








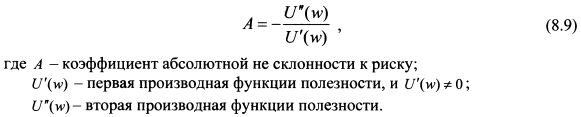

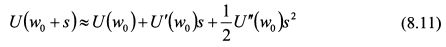
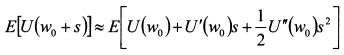
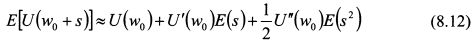
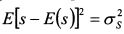 , т.е. дисперсию дохода актива S. Поэтому выражение (8.12) принимает вид:
, т.е. дисперсию дохода актива S. Поэтому выражение (8.12) принимает вид:
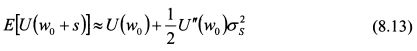

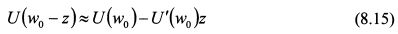
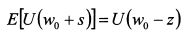
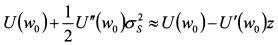
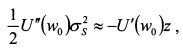
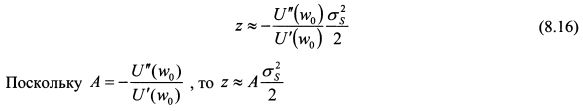
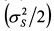 является постоянной величиной. Поэтому абсолютную не склонность риска инвестора можно измерить отношением второй и первой производной его функции полезности, т.е.:
является постоянной величиной. Поэтому абсолютную не склонность риска инвестора можно измерить отношением второй и первой производной его функции полезности, т.е.: 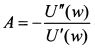 . Можно также отметить, что если функции полезности инвесторов отличаются только на некоторую константу, то их коэффициенты абсолютной не склонности к риску будут одинаковыми, поскольку такие функции имеют одинаковые производные.
. Можно также отметить, что если функции полезности инвесторов отличаются только на некоторую константу, то их коэффициенты абсолютной не склонности к риску будут одинаковыми, поскольку такие функции имеют одинаковые производные.





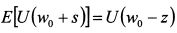
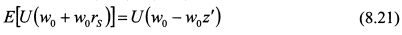
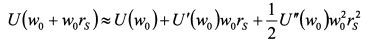
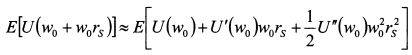
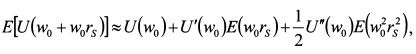
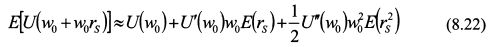
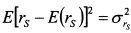 , т.е. дисперсию доходности актива S. Поэтому выражение (8.22) принимает вид:
, т.е. дисперсию доходности актива S. Поэтому выражение (8.22) принимает вид:
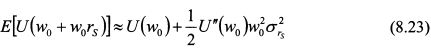
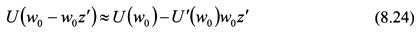
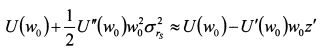
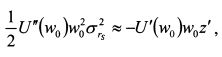

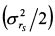 является постоянной величиной. Поэтому относительную не склонность риска инвестора (R), опустив коэффициенты при параметре w, можно определить как:
является постоянной величиной. Поэтому относительную не склонность риска инвестора (R), опустив коэффициенты при параметре w, можно определить как:
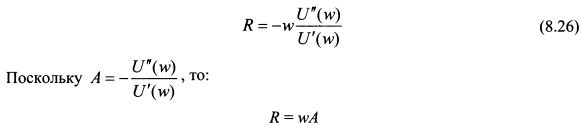


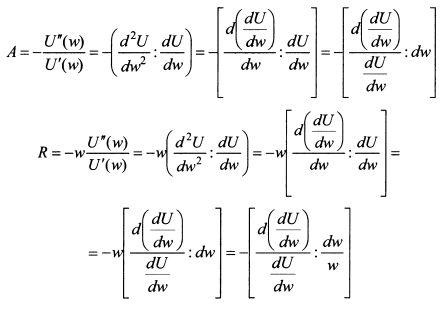
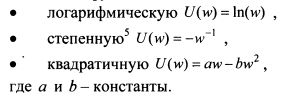

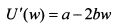
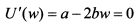
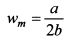
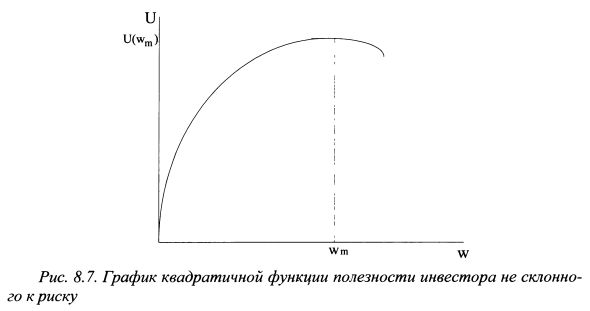
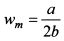 предельная полезность богатства становится отрицательной. В результате убывает общий уровень полезности, что противоречит здравому смыслу, поскольку дополнительное богатство открывает дополнительные возможности для удовлетворения потребностей в разных областях. Если можно допустить полное насыщение вследствие потребления какого-либо товара или услуги и предположить отрицательный эффект от его дальнейшего потребления, то этого нельзя сказать одновременно о всех товарах и услугах. Поэтому рост богатства должен вести к большему уровня полезности. Соответственно необходимо ограничить интервал применения функции отрезком
предельная полезность богатства становится отрицательной. В результате убывает общий уровень полезности, что противоречит здравому смыслу, поскольку дополнительное богатство открывает дополнительные возможности для удовлетворения потребностей в разных областях. Если можно допустить полное насыщение вследствие потребления какого-либо товара или услуги и предположить отрицательный эффект от его дальнейшего потребления, то этого нельзя сказать одновременно о всех товарах и услугах. Поэтому рост богатства должен вести к большему уровня полезности. Соответственно необходимо ограничить интервал применения функции отрезком 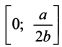 .
.