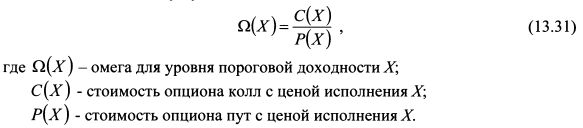|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
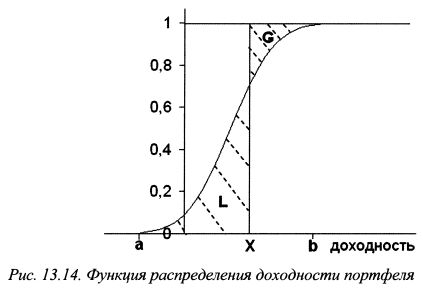
13.4. ОмегаВ параграфе 13.2.5 мы остановились на вопросе сравнительной оценки эффективности портфелей для случая, когда доходности не имеют нормального распределения. В качестве еще одной меры такой оценки может служить показатель омега. Мы рассматриваем данный коэффициент вне параграфа 13.2.5, поскольку омега является более комплексным индикатором. На его основе можно сравнивать как портфели с нормальным распределением доходности, так и с отличными от него распределениями. Кроме того, он позволяет шире взглянуть на проблему выбора инвестором портфеля в сравнении с традиционными подходами, основанными на учете коэффициентов Шарпа, Трейнора, Дженсена или Сортино. Обычно омега покажет другие результаты для портфелей, чем перечисленные выше коэффициенты, поскольку она обладает более полной информацией о распределении доходности портфелей. Данный показатель предложили в 2002 г. C.Keating и W.F.Shadwick. Прежде всего следует отметить, что при расчете данного показателя, как и у коэффициента Сортино, используется некоторый порог доходности, относительно которого инвестор рассматривает свои выигрыши и проигрыши. Для коэффициентов Шарпа и Трейнора - это ставка без риска. Однако у инвестора может быть свой порог допустимой доходности. Он может определяться, например, его склонностью к риску, в том числе в зависимости от возраста, уровнем инфляции, уровнем затрат по формированию портфеля, к которым следует отнести помимо издержек по совершению сделок также и вознаграждение, выплачиваемое менеджерам. Кроме того, минимальный уровень доходности может устанавливать законодательство для определенных категорий институциональных инвесторов. Так, в Швейцарии законом установлена минимальная доходность для пенсионных фондов. Функция омега дает полную характеристику распределения результатов портфеля с точки зрения его риска и доходности. Поэтому, как отмечают C.Keating и W.F.Shadwick, в математическом смысле, она эквивалентна распределению доходности. Омегу можно использовать для сравнительной характеристики разных портфелей без учета функции полезности инвестора. Решения принимаются только на основе одного принципа, что инвестор предпочитает большее меньшему. Пусть порог допустимой минимальной доходности портфеля равен X, и возможные значения его доходности располагаются в диапазоне от а до b. Пусть F(r) - функция распределения доходности портфеля. Тогда возможный выигрыш по портфелю, взвешенный по вероятности, будет равен площади заштрихованной фигуры G, а возможный проигрыш - заштрихованной фигуры L, как показано на рис. 13.14. Отношение G/L можно рассматривать как меру качества инвестиционного выбора. Сравнивая два портфеля на основе данного показателя относительно одинакового порога доходности, следует сделать выбор в пользу портфеля, для которого значение этого отношения больше.
Если возможный выигрыш относительно порога минимальной доходности X равен g, а возможный проигрыш составляет l, то вероятность получить доходность меньше значения X равна F(r). Соответственно вероятность получить доходность больше X составляет 1-F(r). Выигрыш по портфелю, взвешенный по вероятности, равен g[l-F(r)], а убыток, взвешенный по вероятности, составляет lF(r). Отсюда можно записать:
Приблизительно площадь фигуры G = g[l-F(X)] на рис. 13.14 равна площади верхнего прямоугольника G1, на рис. 13.15, а площадь фигуры L = IF(X) соответственно площади нижнего прямоугольника L1. Если мы хотим получить точное значение площадей фигур G и L на рис. b 13.14, то необходимо использовать интегралы. Тогда
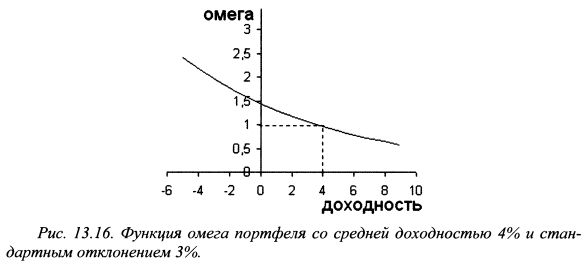
Формула (13.30) представляет собой показатель омега портфеля для порога доходности X. Таким образом, омега (Q) определяется как отношение площади фигуры G к площади фигуры L для порога доходности X. По формуле (13.30) можно найти омегу портфеля относительно любого уровня пороговой доходности на отрезке от а до b. Тогда получим показатель омега как функцию от доходности портфеля &>(г). Поэтому, как отмечают C.Keating, W.F.Shadwick, в математическом смысле функция омега эквивалентна распределению доходности портфеля. В отношении формы данного распределения не требуется никаких параметрических допущений и не накладывается никаких ограничений кроме существования интегралов Омега представляет собой монотонно убывающую гладкую функцию как показано на рис. 13.16. Из формулы (13.30) следует, что, независимо от распределения доходности портфеля, в точке его средней доходности значение омеги равно единице. На рис. 13.16 представлена функция омега доходности портфеля со средним значением 4% и стандартным отклонением 3%. Соответственно для доходности 4% значение омеги равно единице.
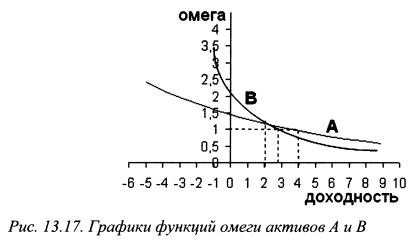
С помощью функции омеги можно сравнить разные активы или портфели. Поскольку омега эквивалентна распределению доходности актива, то на ее основе инвестор может принять более осознанное решение о предпочтении одного актива (портфеля) другому активу (портфелю). Дело в том, что для разных уровней доходности динамика доходности активов с учетом возможного риска будет меняться. Эта информация непосредственно не присутствует в традиционных показателях оценки активов (портфелей), поскольку они основаны прежде всего на учете начальных моментов распределения доходности, т.е. средних значений и дисперсий. Омега учитывает помимо начальных и более высокие моменты распределения доходности. Поэтому она даст более точные результаты для активов (портфелей), в отношении доходностей которых более высокие моменты распределения имеют существенное значение. В тех случаях, когда они не имеют большого значения, омега покажет результаты близкие к традиционным показателям. На рис. 13.17 представлены графики функций омеги активов А и В. На их основе инвестор может принять более точное решение о выборе актива А или В в зависимости от своей склонности к риску. Графики пересекаются в точке доходности равной 2%. Это означает, что в этой точке инвестор безразличен в выборе актива А или В.
Для диапазона доходности вправо от 2% предпочтение следует отдать активу А, так как его функция омеги расположена выше функции омеги актива В. Для диапазона доходности слева от 2% предпочтительнее актив В. В заключение данного параграфа можно отметить, что, как показали H.Kazemi, T.Schneeweis и R.Gupta, коэффициент омега для каждого данного уровня пороговой доходности можно представить как отношение стоимости опциона колл к опциону пут, выписанных на оцениваемые инвестиции:
Опционы имеют одинаковые цены исполнения и истекают в один и тот же момент времени. В то же время, как отмечают авторы, цены опционов следует рассчитывать не на основе принятого подхода в рамках риск-нейтральной вероятности, а использовать действительную вероятностную меру, которой характеризуются оцениваемые инвестиции.
|
||||||||||||
|
|
||||||||||||








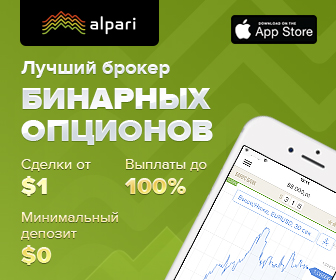
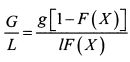
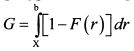 и
и 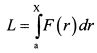 , и отношение G/L соответственно принимает вид:
, и отношение G/L соответственно принимает вид:

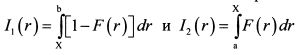 . Это не представляет проблемы для аналитических распределений, определенных на бесконечном интервале. Это также не представляет сложности и на практике, поскольку статистические данные получают на основе дискретных наблюдений значений доходности. Важно подчеркнуть, что функция омега непосредственно рассчитывается на основе наблюдаемых значений доходности, поэтому она включает всю информацию, которую содержит само распределение доходности, и она настолько же статистически значима насколько значим и сам ряд распределения доходности портфеля.
. Это не представляет проблемы для аналитических распределений, определенных на бесконечном интервале. Это также не представляет сложности и на практике, поскольку статистические данные получают на основе дискретных наблюдений значений доходности. Важно подчеркнуть, что функция омега непосредственно рассчитывается на основе наблюдаемых значений доходности, поэтому она включает всю информацию, которую содержит само распределение доходности, и она настолько же статистически значима насколько значим и сам ряд распределения доходности портфеля.