|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
1.2.6. Риск портфеля, состоящего из нескольких активовВыше мы рассмотрели портфель, состоящий из двух бумаг, и сделали общие выводы относительно его формирования. Данные выводы верны и для портфеля, объединяющего большее количество активов. Рассмотрим, как определяется риск портфеля, состоящего из нескольких бумаг. Он рассчитывается по формуле:
В формуле (1.30) стоит знак двойной суммы В итоге получим п слагаемых. Чтобы проиллюстрировать использование данной формулы, рассчитаем риск портфеля, состоящего из трех бумаг. Если портфель будет состоять из большего количества активов, техника расчета останется такой же. Пример 1.
Определить риск портфеля. Решение. Дисперсия портфеля равна:
Стандартное отклонение портфеля составляет:
Как было отмечено выше, для портфеля, состоящего из двух активов с корреляцией доходностей +1, риск представляет собой средневзвешенный риск входящих в него активов. Поэтому для такого случая не наблюдается уменьшение риска, т.е. уменьшение его дисперсии, а происходит только его усреднение. Данный принцип сохраняется и для портфеля, насчитывающего много бумаг с корреляцией доходности +1. Если портфель состоит из активов с корреляцией равной нулю, его риск рассчитывается по формулам:
и
Когда бумаги имеют одинаковую дисперсию и уд. вес, формулу (1.31) можно преобразовать следующим образом:
или
Соответственно формула (1.32) принимает вид:
Как следует из формул (1.33) и (1.34), риск портфеля убывает по мере увеличения количества входящих в него активов. Формулу (1.30) можно переписать в следующей форме:
Если в портфель включить бумаги в равном удельном весе, формула (1.35) запишется как:
или
или
Умножим и разделим второе слагаемое формулы (1.36) на (n-1) и преобразуем его:
В выражении (1.37) величина
При увеличении количества активов в портфеле значение первого слагаемого в формуле (1.38) будет уменьшаться и при большом значении n оно приблизится к нулю. У второго слагаемого выражение
Таким образом, при включении в портфель большого количества бумаг и при условии, что их уд. веса приблизительно одинаковы, риск портфеля по своей величине близок к значению средней ковариации доходностей входящих в него активов. В настоящей главе мы рассчитывали риск портфеля на основе формулы (1.30). Однако следует отметить, что в современной литературе вместо данной формулы часто используется ее аналог, записанный в матричной форме. Поэтому рассмотрим вопрос расчета риска портфеля с помощью матриц. Необходимые сведения из матричного исчисления приведены в приложении 4 к настоящей главе. Риск портфеля ценных бумаг, представленный дисперсией его доходности, с помощью матриц можно записать как:
В качестве иллюстрации использования формулы (1.39) возьмем условия примера 1 настоящего параграфа. Запишем состав каждой матрицы:
В матрице Q по диагонали расположены дисперсии доходностей активов, а оставшиеся элементы представляют собой ковариации доходностей бумаг между собой. Риск портфеля равен:
Осуществим вычисления в формуле (1.40) последовательно:
и
Стандартное отклонение составляет:
Матрица ковариаций Q равна SPS, где Р - корреляционная матрица размера пхп ; ? - матрица стандартных отклонений размера пхп; п - количество активов в портфеле. Поэтому формулу (1.39) можно представить еще следующим образом:
Данная формула для двух активов раскрывается следующим образом:
В заключение следует сказать, что матрицу столбец также часто называют вектором. Поэтому можно сказать, что в формуле (1.41) выражение |
||||||||||||
|
|
||||||||||||









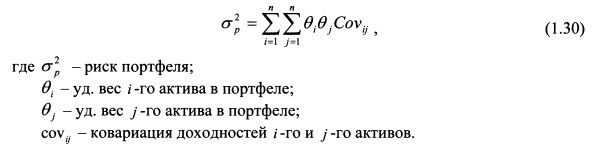
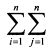 . Это означает, что, раскрывая его, мы должны вначале взять значение i = 1 и умножить на него все значения j от 1 до п. Затем повторить данную операцию, но уже для i = 2, и т.д.
. Это означает, что, раскрывая его, мы должны вначале взять значение i = 1 и умножить на него все значения j от 1 до п. Затем повторить данную операцию, но уже для i = 2, и т.д.
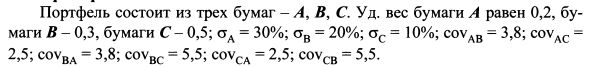
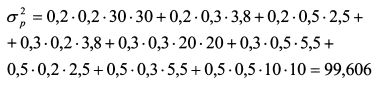
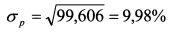


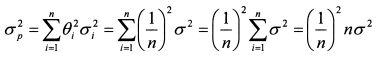


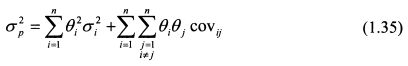
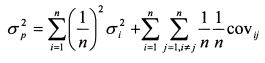
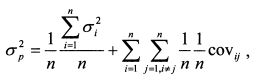

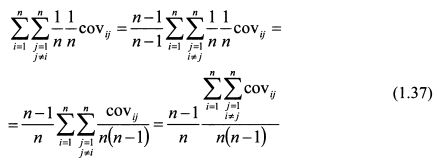
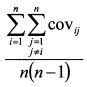 представляет собой среднюю ковариацию доходностей активов, входящих в портфель, так как в ее числителе стоит сумма ковариации, а в знаменателе - их число. Обозначим среднюю ковариацию через
представляет собой среднюю ковариацию доходностей активов, входящих в портфель, так как в ее числителе стоит сумма ковариации, а в знаменателе - их число. Обозначим среднюю ковариацию через 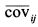 . Тогда формулу (1.35) можно записать как:
. Тогда формулу (1.35) можно записать как:

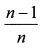 будет стремиться к единице. Поэтому формула (1.38) принимает вид:
будет стремиться к единице. Поэтому формула (1.38) принимает вид:
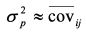

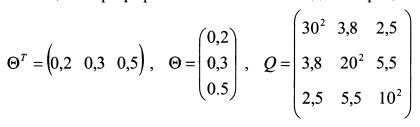



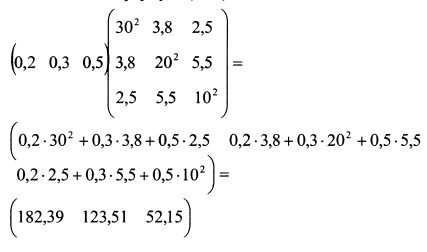

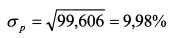
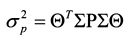

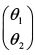 представляет собой вектор удельных весов активов в портфеле, а
представляет собой вектор удельных весов активов в портфеле, а 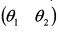 – транспонированный вектор уд. весов.
– транспонированный вектор уд. весов.