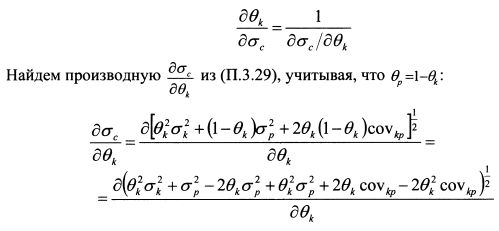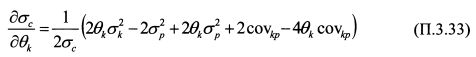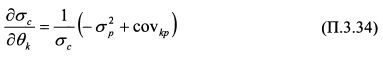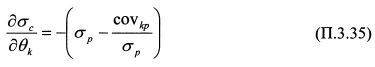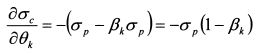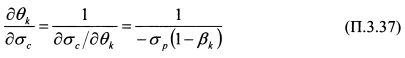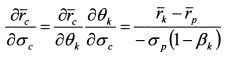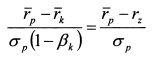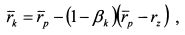|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
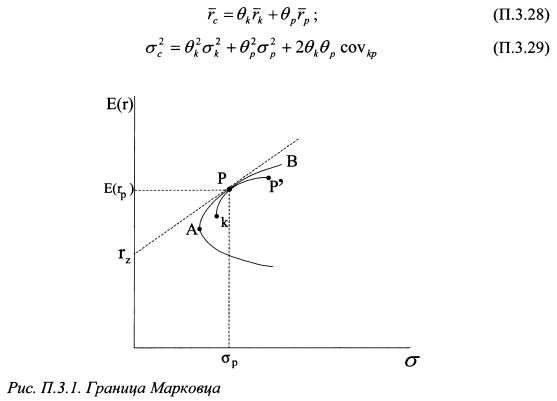
Приложение 2. Зависимость между бетами и ожидаемыми доходностями активов для случая, когда беты определяются относительно любого портфеля на эффективной границе МарковцаВ модели САРМ зависимость между бетами активов и их ожидаемыми доходностями является линейной. Беты определяются относительно рыночного портфеля. Рыночный портфель располагается на эффективной границе Марковца. Докажем в настоящем приложении общий случай, который говорит о том, что линейная зависимость между бетами активов и их ожидаемыми доходностями является линейной, если все беты рассчитаны относительно любого портфеля на эффективной границе Марковца. На рис. П.3.1 представлена граница Марковца для случая коротких продаж. На эффективной границе АВ выбран некоторый портфель Р. К нему проведена касательная, которая пересекает ось ординат графика в точке rz. На рисунке также представлена некоторая бумага к. Поскольку портфель Р расположен на границе Марковца, то данная бумага входит в него в некотором положительном или отрицательном уд. весе. Поэтому кривая kF, которая показывает комбинации бумаги к с портфелем />, является касательной к эффективной границе Марковца в точке Р. Задача состоит в том, чтобы определить зависимость между портфелем Р и бумагой к. Бумага к уже входит в портфель />, поэтому, чтобы отделить ее для целей нашего доказательства от портфеля Р, будем считать, что бумага к представляет собой долю средств сверх той суммы, на которую она уже входит в портфель Р. Теперь рассмотрим новый портфель С. Он является сочетанием портфеля Р и бумаги к ( в нашем новом определении) и располагается на дуге kF. В точке Р уд. вес бумаги к в портфеле С равен нулю, на дуге от точки к до точки Р он положителен, на дуге от точки Р до точки Р отрицателен. Ожидаемая доходность и риск портфеля С соответственно равны:
Ожидаемую доходность портфеля С можно рассматривать как функцию риска. При изменении риска портфеля изменяется и его ожидаемая доходность. Данный процесс опосредуется промежуточной зависимостью уд. веса актива к от риска портфеля. Поэтому ожидаемую доходность портфеля можно представить как сложную функцию от риска портфеля:
Найдем значения производных
Производную
с решениями:
Брать производную
Функцией обратной (П.3.31) является функция (П.3.29). Однако выражение (П.3.32) показывает не однозначное соответствие между ними. Чтобы воспользоваться теоремой об обратной функции, сузим область значений функции (П.3.31 ) в окрестности точки Р для получения на ней однозначного соответствия между функциями (П.3.29) и (П.3.31). Для данной области производная
или
Производная (П.3.33) показывает, как изменится риск портфеля С при изменении уд. веса актива к. В точке Р уд. вес актива к в портфеле С равен нулю. Поэтому производная (П.3.33) в этой точке равна:
В точке Р риск портфеля С равен риску портфеля Р, т.е. сгс —<Ур-. Заменив в формуле (П.3.34) ас на ар и разделив на ар , получим:
Бета актива k относительно портфеля Р составляет:
Выразим из (П.3.36) ковариацию актива к относительно портфеля Р и подставим ее значение в (П.3.35):
Отсюда:
Подставим найденные значения производных в (П.3.30):
или
Производная (П.3.38) определена в точке P, и поэтому показывает угловой коэффициент наклона касательной, проведенной к эффективной границе в этой точке, т.е. угловой коэффициент наклона прямой rzP. В свою очередь из графика на рис. П.3.1 угловой коэффициент наклона данной прямой также равен:
Приравнивая (П.3.38) и (П.3.39), получим:
ИЛИ
или
Уравнение (П.3.40) показывает, что между ожидаемой доходностью актива А: и ее коэффициентом бета, рассчитанным относительно эффективного портфеля Р, существует линейная зависимость. Поскольку бумага к и портфель Р были выбраны произвольно, то линейная зависимость характеризует все активы и их беты, определенные относительно эффективных портфелей.
|
||||||||||||
|
|
||||||||||||









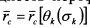 . Возьмем производную ожидаемой доходности портфеля С по стс с учетом сказанной зависимости:
. Возьмем производную ожидаемой доходности портфеля С по стс с учетом сказанной зависимости:

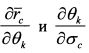 . Из формулы ожидаемой доходности портфеля (П.3.28) с учетом того, что
. Из формулы ожидаемой доходности портфеля (П.3.28) с учетом того, что 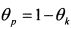 получаем:
получаем:
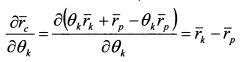
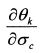 найдем на основе уравнение (П.3.29). Чтобы определить производную в представленной форме, необходимо из уравнения (П.3.29) выразить параметр вк. В результате получим квадратное уравнение
найдем на основе уравнение (П.3.29). Чтобы определить производную в представленной форме, необходимо из уравнения (П.3.29) выразить параметр вк. В результате получим квадратное уравнение
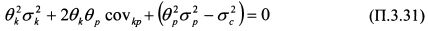
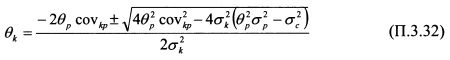
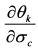 на основе уравнения (П.3.32) не очень удобно. В то же время легко найти производную
на основе уравнения (П.3.32) не очень удобно. В то же время легко найти производную 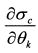 из уравнения (П.3.29). Можно ли на основе производной
из уравнения (П.3.29). Можно ли на основе производной 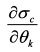 определить производную
определить производную 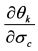 . Можно, если воспользоваться теоремой о производной обратной функции. Данная теорема говорит о том, что между производной функции f(x) и производной обратной ей функции g(y) справедливо равенство:
. Можно, если воспользоваться теоремой о производной обратной функции. Данная теорема говорит о том, что между производной функции f(x) и производной обратной ей функции g(y) справедливо равенство:
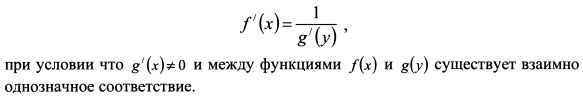
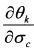 равна:
равна: