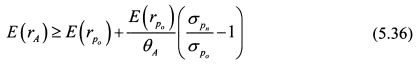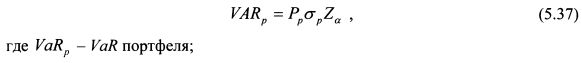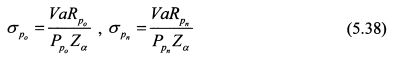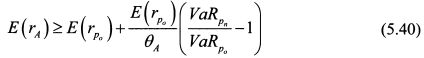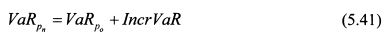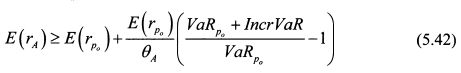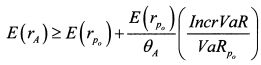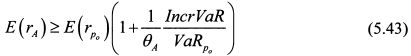|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
5.1.2.5. Выбор актива при пересмотре портфеляПри активном управлении портфелем менеджер периодически будет пересматривать его состав с целью получить более высокую доходность. Одним из способов отбора новых бумаг в портфель может служить правило Шарпа, основанное на использовании коэффициента Шарпа.
В числителе выражения (5.31) представлена ожидаемая доходность актива сверх ставки без риска, т.е. премия за риск, в знаменателе - риск актива. Чем больше данный показатель, тем более привлекателен актив для включения его в портфель. В то же время, поскольку риск портфеля зависит от корреляции доходностей активов, то принять решение о целесообразности включения нового актива в портфель можно, определив коэффициент Шарпа для текущего портфеля и портфеля с новым активом. Коэффициент Шарпа для портфеля рассчитывается по формуле:
Если значение коэффициента для нового портфеля больше чем для текущего, то актив целесообразно включить в портфель. В то же время, если ориентир ожидаемой доходности инвестора остался неизменным, то также должно выдерживаться условие, что ожидаемая доходность нового портфеля не меньше ожидаемой доходности текущего портфеля. В формулах (5.31) и (5.32) в числителе присутствует ставка без риска. Поскольку она является константой для каждого данного момента времени, то инвестиционные решения можно принимать только на основе ожидаемой доходности и риска портфеля (актива). Инвестиционные решения можно принимать также с использованием показателя VaR. Данный подход предложил К.Доуд. Допустим, инвестор решил включить в текущий портфель новый актив А с ожидаемой доходностью Е{гА). Согласно коэффициенту Шарпа, критерий принятия решения о его включении можно записать как:
Уд. вес актива А в новом портфеле составляет вА, уд. вес текущего портфеля в новом портфеле равен \ — 0А. Тогда ожидаемая доходность нового портфеля составит:
Подставим в (5.33) значение ожидаемой доходности нового портфеля:
Если доходности портфелей распределены нормально, то
Из (5.37) стандартные отклонения текущего и нового портфелей соответственно равны:
Если инвестор сохраняет стоимость нового портфеля равной стоимости текущего портфеля, то знаменатели выражений (5.38) являются одинаковыми, поскольку VaR рассчитаны для одинакового уровня доверительной вероятности а. Отсюда отношение стандартных отклонений нового и текущего портфелей равно отношению их значений VaR , т.е.:
Подставим в (5.36) вместо отношения стандартных отклонений портфелей их значение из (5.39):
VaR нового портфеля равен VaR текущего портфеля плюс приростный VaR (lncrVaR), т.е.:
Подставим значение VaR из (5.41) в (5.40):
После преобразования получим:
или
Таким образом, если ожидаемая доходность актива А больше чем правая часть неравенства (5.43) то актив целесообразно включить в портфель.
|
||||||||||||
|
|
||||||||||||












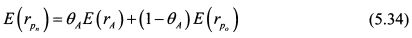
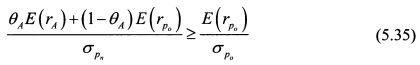 Выразим из (5.35) ожидаемую доходность актива А:
Выразим из (5.35) ожидаемую доходность актива А: