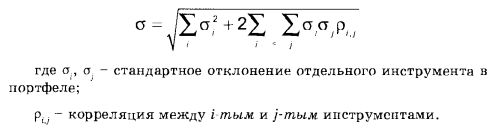|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
Виды расчетов VaRС годами появилось три основных метода расчетов рисковой стоимости: 1. Вариационно-ковариационный (аналитический) метод расчета VaR. Это, наверное, наиболее широко распространенный метод расчета. Он подразумевает, что программа собирает данные о волатильности (вариация) и корреляции (ковариация) для всех отдельных позиций в портфеле и объединяет их, используя матричную алгебру, в едином расчете волатильности портфеля. Основное уравнение, на котором базируется расчет рисковой стоимости с помощью вариационно-ковариационного метода, – это вычисление стандартного отклонения портфеля на основе предположения, что его распределение может считаться многомерным нормальным; то есть отдельные переменные компоненты портфеля (например, торговые позиции) будут вести себя таким образом, что если смотреть на них в совокупности, то они дадут нормальное распределение. В этом случае стандартное отклонение портфеля (о) можно вычислить по следующей формуле:
Не расстраивайтесь, если у вас не получается до конца понять все топкости этой страшноватой формулы. Во-первых, вы должны относиться с некоторым скептицизмом к любым математическим выражениям, в которых содержатся одновременно и маленькие σ, и большие Σ (эти последние, должен признать, выглядят намного круче, если снизу к ним пришпилить крошечные индексы i и j, а еще лучше, если сверху вы можете поставить – как оно часто и бывает – значок ∞). Сейчас я сделаю одно маленькое признание. Я занимаюсь этими игрищами в управление рисками уже около двух десятков лет, и за все это время могу припомнить только один случай, когда мне действительно пришлось вытащить на свет божий эту сомнительную формулу, чтобы хоть как-то успокоить одних до крайности привередливых и насмешливых джентльменов из Японии. Вообще говоря, я думаю, вы можете совершенно спокойно стереть эту формулу из банка данных вашей памяти – то есть, я хочу сказать, вы можете это сделать, если пообещаете мне запомнить следующие факты: Используя сочетание статистических данных о волатильности и корреляции и (тут вам придется мне просто поверить на слово) простого матричного разложения базового расчета стандартного отклонения, мы можем вывести оценку стандартного отклонения для сложного портфеля, которая будет более или менее такой же точной и применимой, как и те, что мы вычисляли для отдельных ценных бумаг. Частично благодаря своей относительной простоте, подход к расчету рисковой стоимости вариационно-ковариационным методом стал наиболее распространенным из всех методов расчета VaR. Он есть почти во всех программных продуктах по управлению рисками, и на самом деле расчет по нему можно произвести относительно просто даже с помощью электронной таблицы – если, конечно, у вас есть соответствующие данные о волатильности и корреляции. В свою очередь, эти данные вы можете либо получить напрямую из ряда источников (например, используя технологию RiskMetrics), либо посчитать их самостоятельно, используя информацию об историческом ценообразовании для каждой позиции, связанной с интересующим вас портфелем, и преобразовать их в ковариационную матрицу. Однако приверженцев принципа «сделай сам» я должен предупредить, что не следует недооценивать сложности задачи, связанной с построением этой матрицы, – эта сложность, в зависимости от количества отдельных позиций в портфеле, будет расти экспоненциально. Например, в матрице для портфеля, в котором содержится, скажем, 10 видов ценных бумаг, будет 100 элементов (10 х 10). Но если количество позиций в портфеле удвоится, то размерность матрицы увеличится вчетверо (20 х 20 = 400). К тому моменту, когда перечень позиций достигнет 100 наименований, в матрице будет уже 10 тысяч отдельных элементов; а если бы вы даже были настолько амбициозны, что захотели бы смоделировать, скажем, ковариационную матрицу для индекса Standard & Poor's 500, то число элементов в такой матрице было бы равно 250.000! В этой связи я настоятельно рекомендую всем, за исключением тех трейдеров, которым нужны очень большие объемы данных, использовать программы для расчета VaR из внешних источников, а если вы должны посчитать вашу собственную рисковую стоимость, вам следует, по крайней мере, взять из внешнего источника ковариационную матрицу. Подход к расчету рисковой стоимости вариационно-ковариационным методом широко используется потому, что по сравнению с другими вариантами расчета VaR он предлагает наименее трудоемкое с точки зрения объема необходимых вычислений средство для определения подверженности портфеля рискам. Однако по этой же причине у него имеется и очень большой набор ограничений. В первую очередь этому методу присущи все недостатки, связанные с потенциальной неточностью основных исходных данных для расчета – то есть данных о волатильности и корреляции; для интересующего нас портфеля они не могут быть точными прогнозирующими параметрами для вычисления будущей модели ценообразования. Во-вторых, этот метод не располагает никакими по-настоящему эффективными средствами, позволяющими работать со сложными производными финансовыми инструментами – например с опционами, данные по которым просто физически невозможно аккуратно и точно «уложить» в ковариационную матрицу. На самом деле, для преобразования этих позиций в какие-то взаимозаменяемые единицы лежащего в их основе базового инструмента большинство программ расчета рисковой стоимости используют простую поправку – скажем, для опционов вводится коэффициент «дельта». Например, с длинным опционом «колл» на акции XYZ на $1 миллион, который имеет дельту, равную 0.5, будут проделаны те же преобразования, что и с позицией на $500,000 на наличном рынке. Поэтому полученные результаты следует интерпретировать с большой осторожностью. Однако, несмотря на эти ограничения, подход к расчету рисковой стоимости вариационно-ковариационным методом, наверное, характеризуется оптимальным соотношением простоты и точности, которая устраивает большинство инвесторов (т.е. выгода от простоты метода более чем компенсирует недостатки, связанные с ограничением его точности). Поэтому для расчета VaR его, наверное, применяют наиболее часто. 2. Метод Исторического Моделирования (историческая волатильность) Этот подход состоит в следующем: программа расчета VaR фактически пересчитывает значение прибылей/убытков для существующего портфеля, каждый день возвращаясь к прошлым показателям, чтобы определить, сколько бы данный счет заработал или потерял за каждый день в последовательности. Затем программа упорядочивает эти наблюдения прибылей/убытков по возрастанию и устанавливает то значение VaR, которое соответствует убытку, связанному с доверительным интервалом, определяемым пользователем. Например, если бы ваша программа расчета VaR по методу исторического моделирования могла производить обзор данных, собранных за год, то она взяла бы текущие данные вашего портфеля, посчитала для него значения прибылей/убытков для каждого дня, всякий раз возвращаясь ровно на 12 месяцев назад, и упорядочила бы полученные статистические данные по возрастанию. Если вы установили доверительный интервал, равный 95%, то программа отбросит худшие 5% значений ваших убытков (за операционный год длиной в 250 дней накопится примерно 12-13 таких наблюдений), и затем установит значение вашего риска на уровне убытков, соответствующем следующему наибольшему значению наблюдений. В основе здесь лежит предположение о том, что вы должны быть на 95% уверены, что в будущем ежедневные убытки этой цифры не превысят. Расчет VaR по методу исторического моделирования является очень трудоемким с точки зрения объема необходимых вычислений, поскольку требует переоценки каждого отдельного инструмента за каждый отдельный день выбранного исторического отрезка времени. Однако я думаю, что если выполнить такой расчет возможно, то затраченные на это ресурсы вполне того стоят, поскольку метод исторического моделирования считается наиболее точным из всех методов расчета VaR – по крайней мере, для подавляющего большинства портфелей. Подтвердить его основные преимущества поможет внимательное рассмотрение той идеологии, которая лежит в его основе. Во-первых, для оценки размера соответствующей подверженности рискам метод исторического моделирования фактически использует данные об историческом ценообразовании, а не полагается на данные о корреляции, чтобы на их основе приписать нескольким ценным бумагам определенные свойства ценообразования по отношению друг к другу. Это может быть особенно важным во времена рыночных стрессов, когда склонны давать сбои даже модели статической корреляции. Во-вторых, в отличие от вариационно-ковариационного, метод исторического моделирования можно логически распространить и на такие производные инструменты, как опционы (при условии, что пользователь тщательно и аккуратно введет в программу весь набор входных данных), причем зачастую результаты расчета очень наглядно и изящно иллюстрируют ту причину, по которой многие менеджеры по управлению рисками, имеющие возможность выбирать для себя оптимальный метод расчета VaR, предпочитают именно этот метод. Наконец, метод исторического моделирования обеспечивает все возможности для проведения качественного анализа показателей на фоне реальных рыночных событий. Если в полученных результатах вас что-то заинтересовало, то очень полезно повнимательнее посмотреть на конкретные даты, в которые произошло нечто, что к таким результатам привело. Другие виды расчета VaR такого аналитического инструмента не обеспечивают. Постарайтесь воспользоваться его преимуществами – оцените вероятность повторения определенных событий и, может быть, попытайтесь даже составить соответствующий план на случай непредвиденных дополнительных обстоятельств. Ограничения, которые являются обязательными для метода исторического моделирования, характерны также и для любой другой статистической оценки подверженности портфеля рискам. Как мы уже говорили, они связаны с тем, что исторические данные не могут служить основанием для надежного предсказания будущих результатов. Кроме того – и об этом мы тоже уже упомянули, – этот метод требует большого объема вычислений, и, в принципе, помимо практических трудностей выполнения рутинных расчетов, он, наверное, более подвержен ошибкам погрешности, чем другие модели. Одно неправильное значение может существенно повлиять на конечный результат, даже если все остальные элементы расчета (который может включать сотни и тысячи отдельных шагов вычислений) абсолютно правильны. Однако если вы в состоянии преодолеть эти проблемы, то я очень рекомендую пользоваться этим методом всегда, когда имеющиеся исходные данные и соответствующие программные средства позволяют вам это сделать. 3. Метод Статистического Моделирования (метод Монте-Карло). Подход к расчету VaR по методу Монте-Карло похож на тот метод Монте-Карло, который применяется для вычисления модели ценообразования опционов. В соответствии с этим методом, программа генерирует большие объемы случайных чисел, имитирующих реально возможные результаты изменения цен отдельной ценной бумаги (на основе определяемого пользователем набора сценариев) и затем статистически классифицирует их в соответствии с их вероятностью. Затем программа присваивает VaR значение, привязанное к заданному доверительному интервалу. Например, программа расчета VaR по методу Монте-Карло для фиксации риска в 95-процентном доверительном интервале может переоценивать целые портфели до нескольких миллионов раз, чтобы определить весь диапазон возможных значений прибылей/убытков и затем установить такое значение VaR, чтобы значения 95% наблюдений были меньше этой цифры, а оставшиеся 5% – больше ее. Преимущество моделирования по методу Монте-Карло состоит и том, что с помощью строгой экстраполяции рыночной истории по огромному числу результатов можно получить лучшую картину полного возможного распределения цен для данного портфеля, и, таким образом, иметь больший объем информации в отношении вероятностей возникновения широкого спектра возможных результатов. Кроме того, метод Монте-Карло может быть полезен для портфелей с большим количеством опционов: он предусматривает оценку практически неограниченного числа сочетаний цен и волатильностей лежащих в основе опционов базовых инструментов, а это является хорошей базой для определения стоимости опционов, содержащихся в данном портфеле, – в том числе и тех, что связаны с наиболее жесткими рыночными условиями, способными вызвать резкое колебание стоимости портфеля. Однако моделирование по методу Монте-Карло для большинства простых портфелей, наверное, будет чересчур мощным орудием любое увеличение точности становится в этих случаях просто несопоставимым с теми издержками, которые связаны с повышением уровня сложности и объемом необходимых для этого вычислений. Стоит отметить, что для всех, кроме наиболее сложных портфелей с очень тонкими характеристиками ценообразования, результаты расчета VaR по всем трем описанным методам должны вполне соответствовать друг другу. На самом деле, я думаю, гораздо важнее потратить свое время на то, чтобы просто ввести расчет VaR в практику, чем транжирить ресурсы, выбирая, какой именно метод предпочесть. Выберите тот, который вам кажется наиболее подходящим с учетом характеристик вашего портфеля и ограничений, налагаемых на имеющиеся ресурсы, и включите его в свой процесс принятия решений. Остальное, как говорится, несущественно.
|
||||||||||||
|
|
||||||||||||