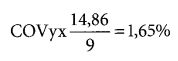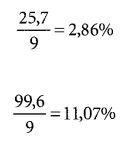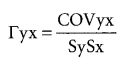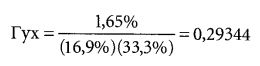|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
Более точная оценка взаимосвязиЕсли использовать только информацию о том, превысило или нет данное значение среднее для этой переменной, теряется много информации. Можно использовать более точную меру корреляции, которая учитывает не только знак, но и величины отклонения от средних. Наиболее популярным методом измерения связи двух переменных является коэффициент корреляции. Этот коэффициент вычисляется при помощи расчета ковариации (совместной вариации) двух переменных. Вот его формула:
где Гух – коэффициент корреляции, a S – стандартные отклонения. Ковариация между Y и X определяется по следующей формуле:
Вот последовательность расчета ковариации двух переменных:
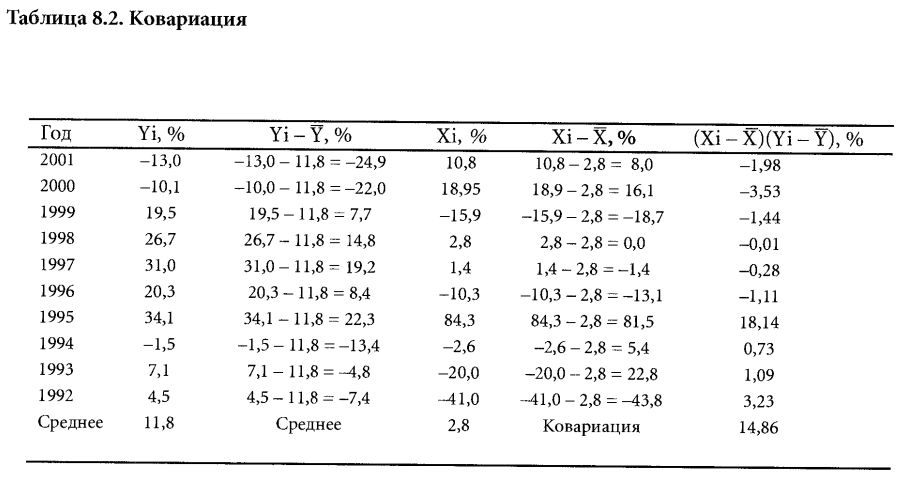
В табл. 8.2 показан этот расчет для процентных ставок и доходности S&P 500 за последние 10 лет. Таким образом, ковариация между Y и X равна 14,86, деленным на 10 лет минус 1, или на 9 (девять степеней свободы).
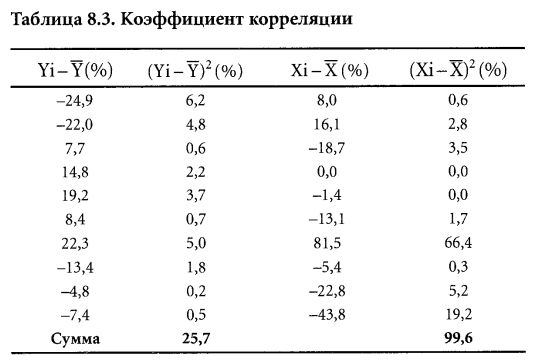
Для того чтобы рассчитать на основе этого значения ковариации коэффициент корреляции, посчитайте стандартные отклонения Y и X. Для этого нужно возвести в квадрат отклонения от среднего для каждой переменной и затем сложить результаты (табл. 8.3).
Дисперсии переменных равны этим суммам, деленным на (n-1):
Для того чтобы получить стандартные отклонения, нужно извлечь из дисперсий квадратный корень. Квадратный корень из 2,86% равен 16,9%, а квадратный корень из 11,07% равен 33,3%. Затем следует подставить полученные результаты в исходную формулу:
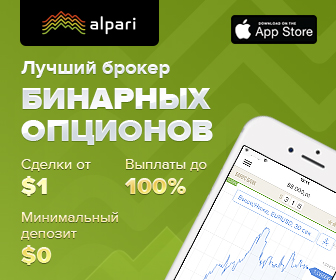
Вот более элегантный способ записи формулы для коэффициента корреляции:
Точно так же, как и для грубой оценки корреляции, которую мы получили из четырехклеточной таблицы, расчеты числителя и знаменателя приведенной выше формулы были основаны на отклонениях наблюдений от средних значений.
|
||||||||||||
|
|
||||||||||||








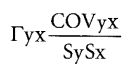
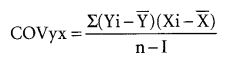 где
где