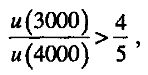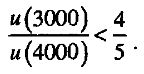Определенность, вероятность и возможность

В рамках классической теории полезности исходы оцениваются вероятностью их реализаций. Ряд экспериментов позволит убедиться в том, что предпочтения людей систематически нарушают этот принцип.

Для начала покажем, что люди переоценивают полезность исходов, которые рассматриваются ими как известные наверняка, по отношению к исходам, имеющим какую-то вероятность, – феномен, известный как эффект наверняка [certainty effect].

Впервые этот контрпример теории ожидаемой полезности был предложен экономистом Морисом Аллаисом в 1953 г. Следующая пара альтернатив является вариацией примера, приведенного в работе Аллаиса, и отличается от оригинала лишь тем, что в них используются менее экстремальные числа. Число, обозначающее процент тех, кто выбрал данную альтернативу, заключено в квадратные скобки.

Проведенный тест показал: 82% респондентов выбрали вариант В в проблеме 1; 83% респондентов – вариант С в проблеме 2. Подобное распределение предпочтений грубо нарушает аксиомы теории ожидаемой полезности. При условии, что м(0) = 0, в проблеме 1 было установлено следующее неравенство:

м (2400) > 0,33м (2500)+0,66м (2400)

или

0,34и (2400) > 0, 33u (2500),

в то время как в проблеме 2 было установлено диаметрально противоположное неравенство:

0,33м (2500) > 0,34м (2400)

или, используя другую запись,

2400>2500 х 0,33+2400 х 0,66

или

2400 х 0,34 = 816>825 = 2500 х 0,33;

2500 х 0,33 = 825>816 = 2400 х0,34.

Не правда ли, любопытный результат?

Проблемы 3 и 4 иллюстрируют тот же феномен, используя более простые формулировки.

В проблемах 3 и 4, как и во всех остальных проблемах, рассматриваемых в этом разделе, более чем половина всех респондентов нарушает теорию ожидаемой полезности. Для того чтобы доказать это нарушение в проблемах 3 и 4, предположим, что u(0) = 0. Теперь заметим, что выбор В устанавливает следующее неравенство:

в то время как выбор С устанавливает диаметрально противоположное неравенство:

Заметим также, что перспектива С = (4000, 0,2) может быть переписана как (А 0.25)г в то время как перспектива D = = (3000, 0,25) может быть записана в виде (В, 0,25).

Одна из аксиом теории ожидаемой полезности гласит, что если В предпочтительней А, то тогда (для любой вероятности) (В, р) должна быть предпочтительней (А, р). Очевидно, что наши объекты не подчиняются этой аксиоме. Также очевидно, что снижение вероятности выигрыша с 1 до 0,25 оказывает намного более значительное влияние на предпочтения, нежели ее снижение с 0,8 до 0,2.

Проблемы выбора 5 и 6 иллюстрируют эффект «наверняка» на неденежных исходах.

Эффект «наверняка» не единственный нарушитель аксиом теории ожидаемой полезности.

В проблемах 7 и 8 можно найти еще одного нарушителя. Проблема 7. Сделайте выбор между двумя альтернативами:

Заметим, что в проблеме 7 вероятности выигрыша значительны (0,9 и 0,45) и большинство людей выбрало перспективу, обладающую наибольшей вероятностью выигрыша.

В проблеме 8 существует возможность выигрыша, но вероятности выигрыша мизерные (0,002 и 0,001). В подобной ситуации, когда выигрыш возможен, но маловероятен, большинство людей выбирает перспективу, предлагающую наибольшую прибыль.

Вышеприведенный пример иллюстрирует общее для большинства людей отношение к риску или шансу, которое не может быть объяснено в рамках теории ожидаемой полезности. Подобное нарушение аксиом ожидаемой полезности может быть формализовано следующим образом. Если (р, q) эквивалентно (х, р), то тогда (у, pqr) предпочтительней (х,pr), где 0 < р, q, г < 1. Это свойство будет ниже интегрировано нами в альтернативную теорию принятия решений.

Содержание

Далее