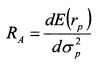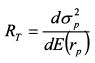|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
8.1.5. Кривая безразличияВыше было сказано, что аргументами функции ожидаемой полезности инвестора являются ожидаемая доходность от осуществляемых инвестиций и ее дисперсия. Получим данный результат в несколько более строгой форме. Разложим функцию полезности инвестора в ряд Тейлора до слагаемого второй степени в окрестности точки равной ожидаемой доходности инвестиций:
Возьмем от нее математическое ожидание:
или
В равенстве (8.27) выражение Е\г-г) равно нулю, так как это математическое ожидание отклонения доходности инвестиций от их средней доходности. Выражение Е\г-г) представляет собой дисперсию доходности инвестиций (<т2), поэтому уравнение (8.27) приводится к виду:
Уравнение (8.28) показывает, что ожидаемая полезность инвестора является функцией ожидаемой доходности и риска инвестиций, измеренного дисперсией их доходности. Поэтому в общем виде функцию ожидаемой полезности инвестора Е(и) МОЖНО записать как:
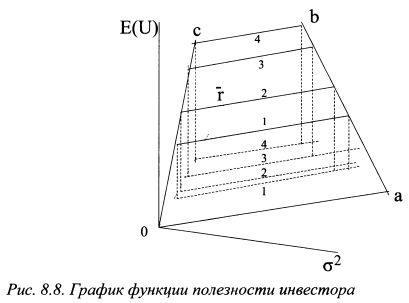
Функция ожидаемой полезности зависит от ожидаемой доходности и дисперсии доходности. Ее график можно представить в трехмерном пространстве, как показано на рис. 8.8. На графике на гори зонтальной плоскости по одной оси откладывается дисперсия доходности инвестиций, по другой - ожидаемая доходность инвестиций, по вертикальной оси - значения функции ожидаемой полезности. Значения функции образуют поверхность aocb. Данную поверхность можно представить в виде набора линий уровня, которые получаются, если разрезать ее горизонтальными плоскостями параллельными плоскости a2 or . Каждая линия уровня характеризуется тем, что значение функции на всем ее протяжении является определенной константой. На графике представлены четыре линии уровня - это сплошные линии под номерами 1, 2, 3 и 4. Линии уровня можно спроецировать на плоскость о1 or . На графике проекции линий уровня обозначены пунктирными линиями с теми же номерами. В экономической теории проекция графика линии уровня называется кривой безразличия, а набор таких проекций - картой кривых безразличия. Таким образом, функцию ожидаемой полезности инвестора можно представить в виде проекций линий уровня на плоскость о1 or, т.е. как карту кривых безразличия. Для анализа поведения инвестора функцию ожидаемой полезности удобно использовать именно в виде карты кривых безразличия.
Каждой линии уровня соответствует постоянное значение функции ожидаемой полезности. Поэтому каждая кривая безразличия характеризуется тем, что уровень ожидаемой полезности, получаемый инвестором от инвестиций, постоянен в любой ее точке. Этим свойством можно воспользоваться, чтобы вывести формулу кривой безразличия. Для этого возьмем полный дифференциал функции (8.28) по входящим в нее переменным F и <т2:
или
(Поскольку для каждой линии уровня ожидаемая полезность является константой, то в уравнении (8.29) dE\U{r)] = 0). Примем третью производную по ожидаемой доходности U'ir) за ноль. Тогда уравнение (8.29) запишется как:
Разделим уравнение (8.30) на U'(r):
Выражение
Тогда формулу (8.31) можно записать как:
Величина обратная RA называется коэффициентом допустимости риска (RT), т. е. С учетом этого формула (8.32) примет вид:
Проинтегрируем уравнение (8.33):
Выразим из него значение ожидаемой доходности:
Уравнение (8.34) является уравнением кривой безразличия. Величина i?[f/(r)j представляет собой точку, в которой график уравнения (8.34) пересекает ось ординат. Она соответствует ожидаемой полезности инвестора для случая, когда риск портфеля равен нулю. Величина
Поскольку коэффициент допустимости риска RT является величиной обратной RA, то он говорит о том, сколько единиц риска готов принять инвестор при увеличении ожидаемой доходности портфеля на одну единицу или, сколько единиц риска приходится на единицу ожидаемой доходности. Соответственно его можно определить как:
Чем больше значение RT, тем меньше вознаграждения в единицах ожидаемой доходности требует инвестор, т. е. на единицу ожидаемой доходности приходится больше единиц риска. Такой инвестор более склонен к риску, и график кривой безразличия является менее крутым. Для каждого уровня ожидаемой полезности 2s[t/(r)j на основании уравнения (8.34) мы получим свою кривую безразличия, соответствующую определенному уровню полезности инвестора. В совокупности они образуют карту кривых безразличия. График карты кривых безразличия представлен на рис. 8.9.
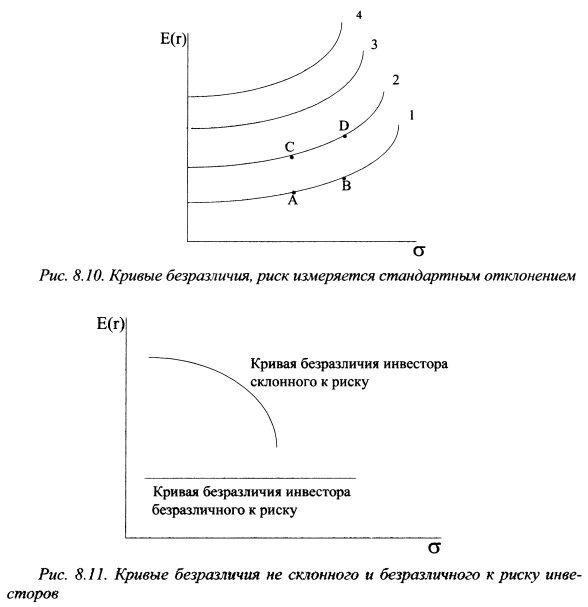
На рис. 8.9 в качестве меры риска принята дисперсия портфеля. Если вместо дисперсии использовать стандартное отклонение, то кривые безразличия примут наиболее характерную для них выгнутую форму, как показано на рис. 8.10. Каждая кривая безразличия характеризуется тем, что в любой ее точке вкладчик получает одинаковую ожидаемую полезность, т. е. различные сочетания риска и доходности на одной кривой обладают для него одинаковой полезностью. Так, ему безразлично, какой актив выбрать А или В (см. рис. 8.10), поскольку оба они приносят ему одинаковую полезность. Более высокая ожидаемая доходность актива В компенсируется его более высоким риском. Аналогично инвестору безразлично, какой актив выбрать на второй кривой безразличия - С или D. В то же время кривые безразличия характеризуются тем, что любой портфель, который расположен на более высокой кривой безразличия, приносит инвестору большую ожидаемую полезность. Так активы С и D предпочтительнее для вкладчика по сравнению с активами Аи В. Если сравнить активы А и С, то риск у них одинаковый, однако ожидаемая доходность актива С выше, поэтому он предпочтительнее для инвестора. Кривые безразличия не могут пересекаться, поскольку каждой из них соответствует свой уровень полезности инвестора.
Выше мы рассмотрели кривые безразличия инвестора не склонного к риску. Форма кривых безразличия склонного и безразличного к риску инвесторов представлена на рис. 8.11.
|
||||||||||||
|
|
||||||||||||









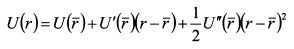
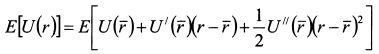

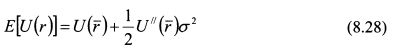
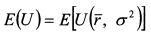
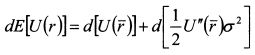
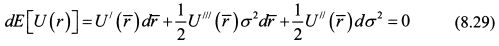
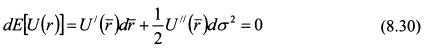
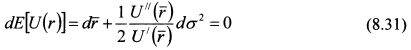
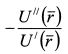 есть коэффициент абсолютной не склонности к риску. Учтем его в формуле (8.31) вместе с сомножителем (1/2) и обозначим через RA:
есть коэффициент абсолютной не склонности к риску. Учтем его в формуле (8.31) вместе с сомножителем (1/2) и обозначим через RA:
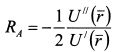
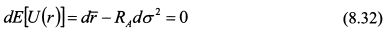
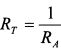 .
. 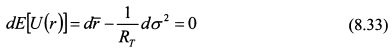
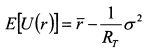

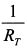 или соответственно RA представляет собой тангенс угла наклона графика к оси абсцисс. Таким образом, коэффициент не склонности к риску измеряет угол наклона кривой безразличия к оси абсцисс, т.е. он измеряет риск в единицах ожидаемой доходности. Он говорит о том, сколько единиц ожидаемой доходности приходится на единицу риска, или на сколько единиц должна возрасти ожидаемая доходность инвестиций для вкладчика, чтобы компенсировать увеличение риска на одну единицу. Чем больше значение RA, тем инвестор менее склонен к риску, и наклон графика кривой безразличия является более крутым. Это означает, что инвестор требует большего вознаграждения при дополнительном увеличении риска. На основе сказанного коэффициент абсолютной не склонности (или неприятия риска) можно определить как:
или соответственно RA представляет собой тангенс угла наклона графика к оси абсцисс. Таким образом, коэффициент не склонности к риску измеряет угол наклона кривой безразличия к оси абсцисс, т.е. он измеряет риск в единицах ожидаемой доходности. Он говорит о том, сколько единиц ожидаемой доходности приходится на единицу риска, или на сколько единиц должна возрасти ожидаемая доходность инвестиций для вкладчика, чтобы компенсировать увеличение риска на одну единицу. Чем больше значение RA, тем инвестор менее склонен к риску, и наклон графика кривой безразличия является более крутым. Это означает, что инвестор требует большего вознаграждения при дополнительном увеличении риска. На основе сказанного коэффициент абсолютной не склонности (или неприятия риска) можно определить как: