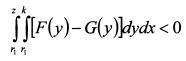|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
Приложение 2. Вывод условий стохастического доминирования портфеляУсловия стохастического доминирования первого порядка (8.54)-(8.55) можно получить на основе следующих рассуждений. Пусть первый портфель с функцией распределения доходности F приносит инвестору большую полезность по сравнению со вторым портфелем с функцией распределения доходности G . Поэтому:
или
или
Проинтегрируем интеграл (П.8.12) по частям. Обозначим u = U(r) и dw = d[F(r)-G(r)]. Отсюда w = F(r)-G(r). Тогда:
Согласно свойствам функций распределения значения вероятностей в крайних точках равны F(rn) = G(rn) = 1 и F(r1) = G(r1) = 0. Поэтому первое слагаемое в правой части (П.8.13) равно нулю. Для выполнения условия (П.8.11) необходимо, чтобы интеграл в правой части (П.8.13) был отрицательным. Поскольку функция полезности инвестора возрастающая и U'(r) > 0, то выражение F(r)-G(r) должно быть меньше нуля. Отсюда следует, что F(r) <= G(r) для всех r и F(r) < G(r) по крайней мере для одного значения r. Критерий стохастического доминирования второго порядка можно получить на основе следующих рассуждений. Первый актив приносит инвестору большую полезность, поэтому:
При доказательстве критерия доминирования первого порядка для данного условия мы получили результат (П.8.13), из которого следовало, что:
Для удобства обозначим интеграл (П.8.14) через I и проинтегрируем его по частям. Обозначим u = U'(r) и dw=[F(r)-G(r)]dr. Отсюда
или
или
По условию U'(rn) > 0, поэтому, чтобы первое слагаемое в правой части (П.8.15) было отрицательным, необходимо выполнение условия:
или
По условию U"(rп) < 0, поэтому, чтобы второе слагаемое в правой части (П.8.15) было положительным, необходимо выполнение условия:
для всех r и
по крайней мере для одного r. Отсюда следует вывод:
для всех r и
по крайней мере для одного r. Критерий стохастического доминирования третьего порядка можно получить на основе следующих рассуждений. Первый актив приносит инвестору большую полезность, поэтому:
При доказательстве критерия доминирования второго порядка для данного условия мы получили результат (П.8.15), из которого следовало, что:
Проинтегрируем второй интеграл в (П.8.16) по частям, обозначив его через J. Обозначим также
ИЛИ
Подставим интеграл (П.8.17) в (П.8.16):
В первом слагаемом неравенства (П.8.18) U'(r) > 0. Интеграл |
||||||||||||
|
|
||||||||||||









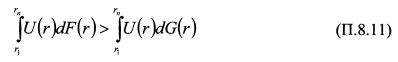
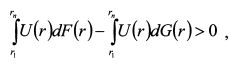

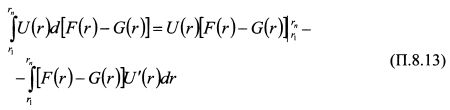
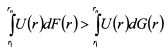

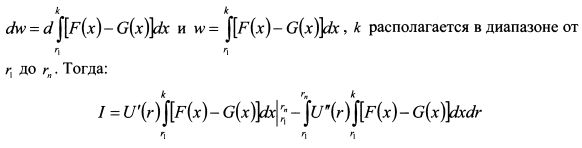
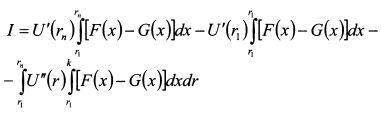
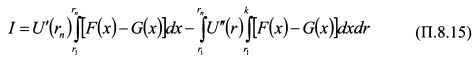
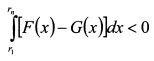
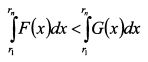
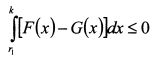
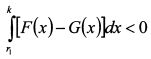
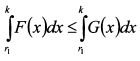
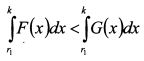


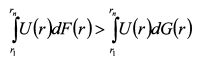
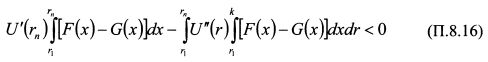
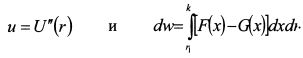 . Отсюда
. Отсюда 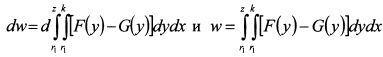 , z располагается в диапазоне от r1 до rn. Тогда:
, z располагается в диапазоне от r1 до rn. Тогда:
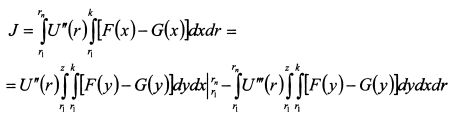
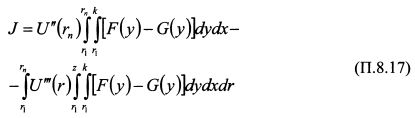
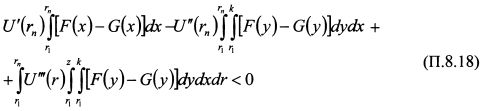
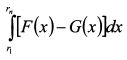 представляет собой разность между средними значениями распределения доходности F и G. По условию среднее значение F меньше G , поэтому интеграл отрицательный. В результате первое слагаемое в (П.8.18) отрицательное. Во втором слагаемом U"(rn) < 0. Следовательно, для того, чтобы оно было положительным, двойной интеграл должен быть отрицательным. В третьем слагаемом U'''(rn) > 0. Чтобы оно было отрицательным, необходимо, чтобы второй интеграл был отрицательным. Таким образом (П.8.18) меньше нуля, если:
представляет собой разность между средними значениями распределения доходности F и G. По условию среднее значение F меньше G , поэтому интеграл отрицательный. В результате первое слагаемое в (П.8.18) отрицательное. Во втором слагаемом U"(rn) < 0. Следовательно, для того, чтобы оно было положительным, двойной интеграл должен быть отрицательным. В третьем слагаемом U'''(rn) > 0. Чтобы оно было отрицательным, необходимо, чтобы второй интеграл был отрицательным. Таким образом (П.8.18) меньше нуля, если: