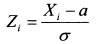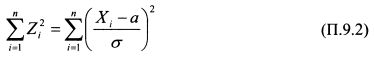|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
Приложение 1. Распределение хи-квадратПусть случайные величины Z1, Z2,..., Zn представляют собой независимые стандартные нормально распределенные величины, т.е. математическое ожидание каждой из них равно нулю и дисперсия равна единице. Сумма квадратов данных случайных величин:
также является случайной величиной. Ее именуют хи-квадрат, а закон ее распределения - хи-квадрат распределением. Данное распределение определяется одним параметром - числом степеней свободы k. Число степеней свободы представляет собой разность между числом суммируемых случайных величин и числом линейных связей, которые ограничивают свободу их изменения. Поскольку в сумме (П.9.1) все слагаемые независимы, т.е. каждая составляющая может менять свое значение независимо от других значений, то число степеней свободы данной случайной величины
Пусть теперь имеется выборка из генеральной совокупности нормально распределенной случайной величины X. Выборка осуществлялась таким образом, что полученные значения случайной величины независимы. (Их можно рассматривать как независимые нормально распределенные величины, имеющие одинаковое математическое ожидание и дисперсию.) На основе выборки находим математическое ожидание суммы данных величин а и дисперсию а. Центрируем и нормируем полученные случайные величины, т.е. вычитаем из каждого значения математическое ожидание и делим на стандартное отклонение. В результате получаем случайные величины:
Они являются независимыми с математическим ожиданием ноль и дисперсией единица. Соответственно сумма квадратов данных величин:
имеет распределение хи-квадрат. Однако в отличие от суммы (П.9.1) количество степеней свободы суммы (П.9.2) составляет k = n-1. Количество степеней свободы уменьшилось на единицу, поскольку по своей сути выражение (П.9.2) представляет собой выборочную дисперсию, в рамках которой случайные величины связаны одним линейным соотношением - фиксированным значением найденного математического ожидания. Связанность случайных величин в этом случае означает, что одну из них можно всегда выразить через остальные, что ограничивает свободу изменения этих величин. Распределение хи-квадрат используется при построении доверительных интервалов для дисперсии.
|
||||||||||||
|
||||||||||||
|
|
||||||||||||
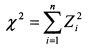равно их количеству, т.е. k = n.
