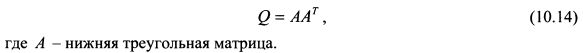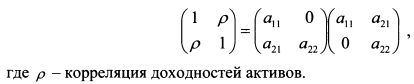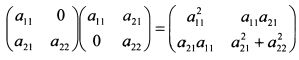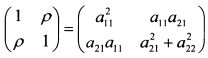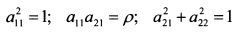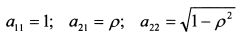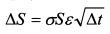|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
10.3.3. Метод Монте-Карло для портфеля из нескольких акцийРассмотрим существо метода Монте-Карло для портфеля из двух бумаг. Для портфеля, включающего большее количество активов, подход останется аналогичным. Распределение стоимости портфеля зависит от степени коррелированности доходностей входящих в него активов. Наиболее просто получить распределение стоимости портфеля, когда доходности акций изменяются независимо друг от друга или когда между ними наблюдается корреляция +1. Как отмечалось в параграфе 10.3.1, изменение цены акции можно смоделировать на основе уравнения (10.3). Поэтому изменение стоимости акций в портфеле можно представить равенствами:
Расчеты применительно к портфелю ценных бумаг удобно осуществлять в матричной форме. Поэтому выражения (10.8) и (10.9) представим в матричной форме как:
Для простоты возьмем в выражении (10.10) период времени равным единице. Тогда оно примет вид:
Учитывая сказанное, цены акций в выражении (10.11) можно представить как:
Стоимость портфеля в конце первого периода можно узнать, умножив выражение (10.12) на вектор количества акций в портфеле:
Формула (10.13) позволяет определить стоимость портфеля, когда корреляция доходностей бумаг равна нулю. Если корреляция доходностей активов в портфеле равна +1 или -1, то выражение (10.13) принимает вид:
Наиболее стандартным является случай, когда корреляция доходностей акций в портфеле отлична от ± 1. Этот факт необходимо учесть при определении его стоимости. Результаты испытаний задаются значениями вектора
Запишем выражение (10.14) для портфеля из двух бумаг:
Произведение матриц ААТ дает результат:
Приравняем элементы корреляционной матрицы и матрицы произведений ААT:
Отсюда:
и
Зададим значения вектора ? как:
Для того чтобы можно было использовать разложение Холецкого, матрица А должна быть положительно определена. Если менеджер включит в модель дисперсии и корреляции, в которых учтены его экспертные оценки, то не исключен вариант, что матрица не будет определена положительно. Точность оценки VaR зависит от количества проведенных испытаний. Возможная ошибка обратно пропорциональна корню квадратному из их количества. В заключение данного параграфа остановимся еще раз на использовании формулы (10.3) для моделирования курсовой стоимости акции. Формула включает элемент juSdt. Он определяет тренд или скорость тенденции движения цены акции. За короткий период времени тренд фактически не определим, и изменение цены акции задается в основном стандартным отклонением. Поэтому, если курс акции моделируется для небольшого периода времени, то данное слагаемое можно опустить. Тогда формула (10.3) примет вид:
Таким образом, для моделирования курса акции для малых периодов времени можно воспользоваться вместо формулы (10.3) выражением (10.16). Разница в результатах тем меньше, чем меньше период времени берется для каждого испытания. При моделировании стоимости акций в портфеле с учетом их корреляций в формуле (10.16) значения е необходимо учитывать в соответствии с выражением (10.15).
|
||||||||||||
|
|
||||||||||||










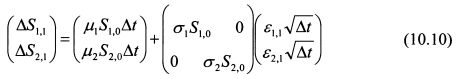


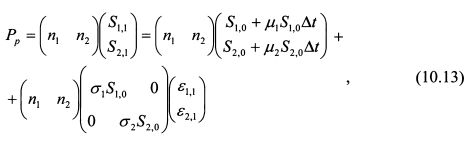

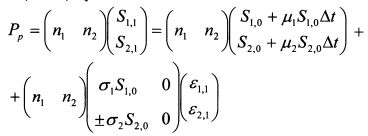
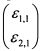 , обозначим его через s. Они должны отражать структуру корреляций доходностей активов. Требуемое условие можно смоделировать, воспользовавшись разложением Холецкого. Разложение Холецкого представляет собой симметрическую матрицу как произведение нижней и верхней треугольных матриц. Поэтому корреляционная матрица портфеля (Q) представима как:
, обозначим его через s. Они должны отражать структуру корреляций доходностей активов. Требуемое условие можно смоделировать, воспользовавшись разложением Холецкого. Разложение Холецкого представляет собой симметрическую матрицу как произведение нижней и верхней треугольных матриц. Поэтому корреляционная матрица портфеля (Q) представима как: