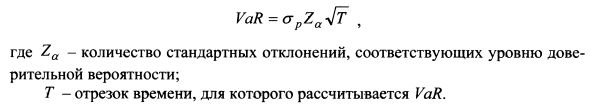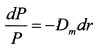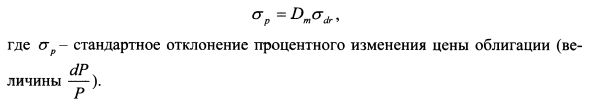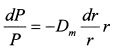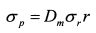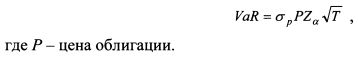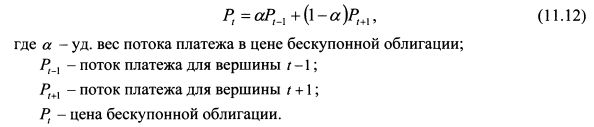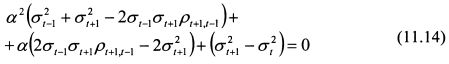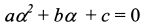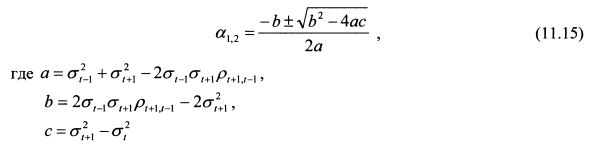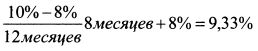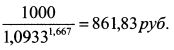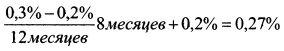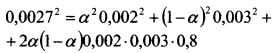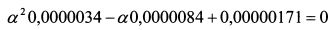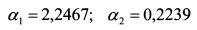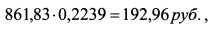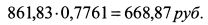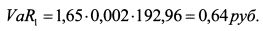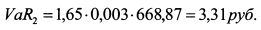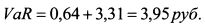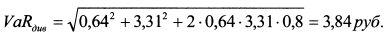|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
11.3. ОблигацииДля небольших изменений процентной ставки определить VaR отдельной облигации можно на основе ее модифицированной дюрации. При таком подходе мы делаем допущение о параллельности сдвигов кривых доходностеи. Как известно, зависимость между изменением цены облигации и изменением ее доходности до погашения приблизительно равна:
На основе уравнения (11.10) можно записать:
В Рискметриках используется несколько иной подход. Равенство (11.10) можно записать как:
Тогда:
Такой поход более согласуется с определением волатильности на рынке, поскольку для финансового актива стандартное отклонение определяют для величины Определив стандартное отклонение цены облигации на основе полученных формул, VaR облигации рассчитаем как:
Формулу (11.10) можно переписать как:
Тогда:
Формулу (11.11) можно представить как:
Тогда:
В таком случае VaR облигации рассчитаем на основе формулы:
На развитом финансовом рынке обращается большое количество облигаций. Поэтому, как и в отношении акций, целесообразно свести все их разнообразие к нескольким стандартным облигациям, на которые можно было бы проецировать облигации в портфеле при расчете VaR. Главным фактором риска по облигации выступает изменение процентной ставки. Конъюнктура процентных ставок описывается кривой доходности или временной структурой процентных ставок. Для аналитических целей используют кривую доходности спот на основе доходности до погашения облигаций с нулевым купоном. Поэтому в качестве стандартных активов для проецирования облигаций используют облигации с нулевым купоном. С увеличением сроков до погашения облигаций дисперсия процентной ставки уменьшается и возрастает корреляция между процентными ставками для соседних временных периодов. Поэтому кривую доходности можно с допустимой точностью приближения представить доходностями бескупонных облигаций для нескольких периодов. В качестве таких периодов можно взять один день, одну неделю, один, три и шесть месяцев, один, два, три, четыре, пять, семь, девять, десять, и тридцать лет. В Рискметриках такими моментами времени выступают один, три, шесть месяцев, один, два, три, четыре, пять, семь, девять, десять, пятнадцать, двадцать и тридцать лет. Выбранные сроки погашения для стандартных бескупонных облигаций называют вершинами (vertices). Они представляют собой факторы риска при описании кривой доходности. Портфель инвестора содержит облигации, которые погашаются не только в стандартные сроки. Поскольку облигации портфеля копируют с помощью данных стандартных бескупонных облигаций, то в этом случае облигации представляют в виде потока платежей (cash flows). Процесс представления позиции в виде потока платежей называется отображением (mapping) . Для бескупонной облигации со сроком погашения отличным от стандартного принцип представления в качестве потока платежей заключается в следующем. Вначале определяют дисконтированную стоимость облигации, т.е. ее цену. После этого цену облигации делят на две части между ближайшими стандартными вершинами. Например, бескупонная облигация погашается через один год и восемь месяцев. Ее цену представят в качестве двух потоков платежей со стандартными сроками один и два года. Для купонной облигации данный принцип сводится вначале к представлению ее в качестве портфеля бескупонных облигаций и затем делению дисконтированной стоимости каждой полученной бескупонной облигации на два потока платежа с двумя стандартными соседними вершинами. Например, купонная облигация номиналом 1000 руб. и купоном 10% погашается через год и восемь месяцев. Купон выплачивается один раз в год. Данная облигация вначале представляется как две бескупонные облигации. Первая с номиналом равным первому купонному платежу, т.е. 100 руб. и погашением через восемь месяцев. Вторая - с номиналом 1100 руб. и погашением через год и восемь месяцев. После этого определяют их дисконтированные стоимости. Затем цену первой бескупонной облигации делят на два потока платежа с вершинами шесть месяцев и один год, второй - на два потока платежа с вершинами один и два года. Для деления цены бескупонной облигации на два потока платежа между соседними стандартными вершинами необходимо найти их удельные веса. Данную задачу решают следующим образом. Цену облигации можно представить как линейную комбинацию потоков платежей:
Чтобы представить дисконтированную стоимость облигации Pt в качестве потоков платежей /)_, и Pt+l, необходимо определить уд. веса а и (\-а). Спроецированная позиция должна иметь такую же дисперсию как и бескупонная облигация. Поэтому уд. веса потоков платежей находят из равенства:
Преобразуем уравнение (11.13) следующим образом:
Уравнение (11.14) является квадратным вида:
Оно имеет два решения:
Поскольку а - это уд. вес потока платежа в цене облигации, то его значение должно лежать в пределах от нуля до единицы. Поэтому в качестве решения уравнения (11.14) из двух значений а следует взять то, которое соответствует указанным границам. Рассмотрим пример определения потока платежей для бескупонной облигации. Пример 1. Бескупонная облигация номиналом 1000 руб. погашается через год и восемь месяцев. Доходность годичной и двухгодичной стандартных бескупонных облигаций соответственно равны 8% и 10%. Однодневное стандартное отклонение процентного изменения цены первой облигации равно 0,2%, второй -0,3%. Коэффициент корреляции между однодневными процентными изменениями цен первой и второй облигаций равен 0,8. Представить облигацию в виде потоков платежей. Решение. Потоки платежей определяются на основе дисконтированной стоимости облигации. Поэтому найдем цену облигации. Для этого необходимо рассчитать ставку дисконтирования. Ставку дисконтирования определяем на основе интерполирования доходности между доходностями годичной и двухгодичной облигаций:
Дисконтированная стоимость облигации равна:
Стандартное отклонение процентного изменения цены облигации определим линейной интерполяцией между стандартными отклонениями процентных изменений цен годичной и двухгодичной облигаций:
Подставим найденные значения в формулу (11.13):
или
Согласно алгоритму (11.15) решения уравнения составляют:
Из двух ответов подходит второй, поскольку он лежит в диапазоне от нуля до единицы. Это означает, что 22,39% стоимости облигации должно приходится на годичную стандартную бескупонную облигацию, а (100-22,39)= 77,61% на двухлетнюю стандартную облигацию. Таким образом, первый поток платежей со стандартной вершиной в один год равен:
второй с вершиной два года:
После того как облигация представлена в виде портфеля потоков платежей для стандартных вершин, VaR определяют обычным способом. Пример 2. Определить однодневный VaR с доверительной вероятностью 95% для бескупонной облигации из примера 1. Решение. В примере 1 облигация была представлена в качестве двух потоков платежей со стандартными вершинами в один год и два года. Определим VaR для первого потока платежа:
VaR для второго потока платежа равен:
Не диверсифицированный VaR бескупонной облигации составляет:
Диверсифицированный VaR равен:
Если мы определяем VaR для купонной облигации, то вначале представляем ее как портфель бескупонных облигаций. После этого дисконтированную стоимость каждой бескупонной облигации делим на два потока платежа между соседними стандартными вершинами. Для каждой вершины суммируем потоки платежей, которые на нее приходятся. Определяем VaR относительно суммарной дисконтированной стоимости каждой вершины. После этого находим VaR купонной облигации на основе VaR вершин. Пример 3. Номинал облигации 1000 руб., купон 10%, выплачивается один раз в год. До погашения облигации один год восемь месяцев. Данную облигацию представляем как две бескупонные облигации: первая с номиналом 100 руб. и погашением через восемь месяцев; вторая - с номиналом 1100 руб. и погашением через один год восемь месяцев. Дисконтированную стоимость первой облигации делим на два потока платежа с вершинами шесть месяцев и один год. Пусть мы получили соответственно потоки 21 руб. и 74 руб. Дисконтированную стоимость второй облигации делим на два потока платежа с вершинами один год и два года. Пусть они соответственно равны 212 руб. и 736 руб. Получили потоки платежей для трех стандартных вершин: шесть месяцев, один год и два года. Первой вершине соответствует поток платежа в 21 руб. На вторую вершину приходятся два потока платежа: 74 руб. по первой облигации и 212 руб. по второй облигации. Суммируем их и получаем 286 руб. На третью вершину приходится поток платежа в 736 руб. Таким образом, купонная облигация представлена в качестве портфеля из трех стандартных бескупонных облигаций с ценами 21 руб., 286 руб., и 736 руб. Далее, как и в предыдущем примере определяем VaR для каждой стандартной бескупонной облигации. Их сумма дает не диверсифицированный VaR. С учетом корреляций между ценами данных облигаций получаем диверсифицированный VaR.
|
||||||||||||
|
|
||||||||||||









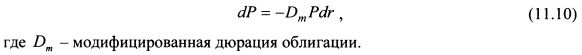
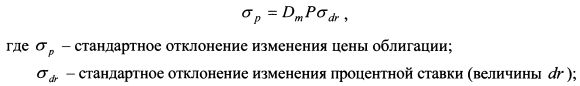

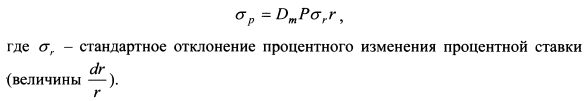
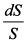 , где S - курс актива.
, где S - курс актива.