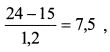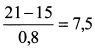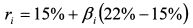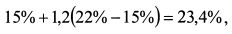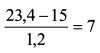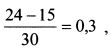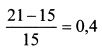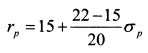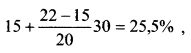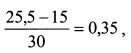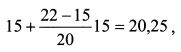|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
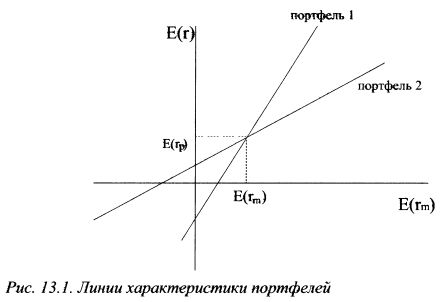
13.2. Показатели эффективности управления портфелем. 13.2.1. Коэффициенты Шарпа, Трейнора и эффективности портфеля облигацийПоказатели доходности и риска представляют собой результаты деятельности менеджера по управлению портфелем. Если сравнивать портфели только на основе их абсолютных значений, то, как правило, сложно получить объективное суждение о мастерстве менеджера. Например, доходность одного портфеля за год составила 50%, второго - 70%. Результаты управления вторым портфелем кажутся более предпочтительными. Однако, если его риск был в два раза больше риска первого портфеля, то более успешным оказался первый менеджер. Неадекватность оценки только на основе показателя доходности для большей наглядности можно проиллюстрировать графически. На рис. 13.1 представлены линии характеристики двух портфелей. Ожидаемая доходность и первого и второго портфелей равна ожидаемой доходности рыночного портфеля. Однако первый портфель имеет более высокое значение коэффициента бета, чем второй. Поэтому его доходность сильнее изменяется при изменении конъюнктуры рынка. Так, в случае экономического подъема он принесет доходность выше доходности второго портфеля. Однако при экономическом спаде его доходность окажется ниже доходности второго портфеля. Поэтому для оценки эффективности управления портфелем используются относительные показатели, учитывающие как его доходность, так и риск.
Показатели эффективности управления портфелем имеют одинаковую структуру. В числителе стоит превышение доходности портфеля над ставкой без риска (rp - rf), поскольку именно данная величина должна выступить в качестве премии за риск портфеля. В знаменателе ставится показатель риска, который может быть или величиной бета, или стандартным отклонением, или (для портфеля облигаций) относительной дюрацией. Первый показатель называют показателем Шарпа. Он равен:
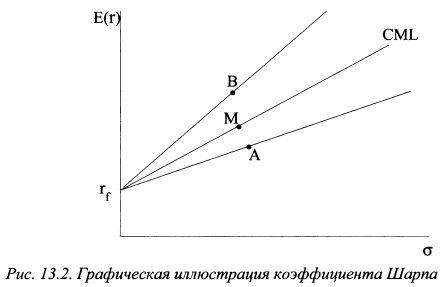
Коэффициент Шарпа учитывает доходность портфеля, полученную сверх ставки без риска, и весь риск, как рыночный, так и не рыночный. Графически, в координатах На рисунке представлена иллюстрация коэффициентов Шарпа для портфелей А и В. По сравнению с рыночным портфелем, расположенном на CML, портфель В управлялся более эффективно, а портфель А менее эффективно.
Коэффициент Шарпа непосредственно следует из уравнения С ML. Уравнение С ML можно переписать следующим образом:
Левая часть равенства (13.6) - это коэффициент Шарпа оцениваемого портфеля, правая часть - коэффициент Шарпа рыночного портфеля. В условиях, когда доходность оцениваемого портфеля равна его равновесной доходности, значение его коэффициента Шарпа равно коэффициенту Шарпа рыночного портфеля. Если оно больше, то менеджер получил более высокое вознаграждение за риск по сравнению с требованием рынка в рамках пассивной стратегии, если меньше, менеджер показал результаты хуже рынка. Второй показатель - это коэффициент Трейнора. Он равен:
В отличие от коэффициента Шарпа в качестве меры риска в нем учитывается бета портфеля. Графически, в координатах
Коэффициент Трейнора непосредственно следует из уравнения SML. Уравнение SML можно переписать следующим образом:
Поскольку коэффициент бета рыночного портфеля равен единице, равенство (13.8) можно представить как:
Левая часть равенства (13.9) - это коэффициент Трейнора оцениваемого портфеля, правая часть - коэффициент Трейнора рыночного портфеля. В условиях, когда доходность оцениваемого портфеля равна его равновесной доходности, значение его коэффициента Трейнора равно величине Третий показатель - коэффициент эффективности портфеля облигаций. В качестве меры риска используется относительная дюрация. Он равен:
Коэффициент Шарпа в качестве меры риска учитывает стандартное отклонение. Поэтому его следует использовать инвестору, портфель которого не является широко диверсифицированным, хотя в общем случае с его помощью можно сравнивать любые портфели, поскольку учитывается весь их риск. Коэффициент Трейнора следует применять лицам с широко диверсифицированным портфелем, поскольку мерой риска здесь выступает величина бета. Если портфели сопоставляются с использованием одного из приведенных выше показателей, то, чем выше его значение, тем лучше результаты управления. Определяя эффективность управления портфелем, целесообразно сделать два сравнения. Во-первых, сравнить его с другими портфелями на основе коэффициентов Шарпа или Трейнора, или коэффициента эффективности облигаций. Во-вторых, сравнить его с результатами рынка, т. е. с аналогичным по степени риска пассивным портфелем. Пример 5. Средняя ставка без риска за некоторый период равна 15%, средняя доходность первого портфеля - 24%, второго - 21%. Бета первого портфеля - 1,2, второго - 0,8. Показатель Трейнора первого портфеля равен:
второго портфеля:
Таким образом, с точки зрения эффективности управления портфели оказались одинаковыми, т.е. на единицу риска менеджеры получили 7,5 единиц вознаграждения. Допустим, что фактическая SML имеет следующее уравнение:
Тогда доходность рынка для риска, соответствующего бете 1,2, т.е. доходность портфеля, расположенного на SML, составила:
а показатель Трейнора:
Для портфеля с бетой 0,8, расположенного на SML, показатель Трейнора также равен 7. Таким образом, в рассмотренном случае активные стратегии позволили получить более высокую доходность по сравнению с равновесной доходностью рынка. Можно предположить, что, поскольку показатели Трейнора для портфелей были выше чем для аналогичных по риску портфелей, расположенных на SML, менеджеры, видимо, получили более высокую доходность за счет правильно выбранного времени покупки и/или продажи активов.
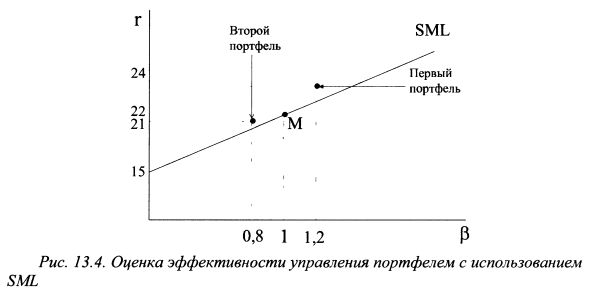
Сравнить портфели друг с другом можно и графически, как показано на рис. 13.4. Здесь представлена фактическая SML, на которой располагаются пассивные портфели. Если сравниваемый портфель находится ниже SML, это означает, что менеджер получил результат хуже рыночного. Если портфель расположен выше SML, то активное управление принесло более высокую доходность чем пассивный портфель с аналогичным уровнем риска. Допустим теперь, что стандартное отклонение доходности первого портфеля составило 30%, второго - 15%. Тогда показатель Шарпа для первого портфеля равен:
для второго:
На основе данных результатов можно сделать вывод о том, что второй портфель управлялся более эффективно: менеджер второго портфеля на каждую единицу риска получил вознаграждение в размере 0,4 единиц доходности, а первого - только 0,3 единиц. Сравним теперь портфели с аналогичными по риску портфелями на С ML. Пусть стандартное отклонение доходности рыночного портфеля равно 20%, и уравнение CML имеет вид:
Тогда доходность портфеля на CML для риска в 30% равна:
а коэффициент Шарпа:
Доходность портфеля на СML для риска в 15%:
а коэффициент Шарпа:
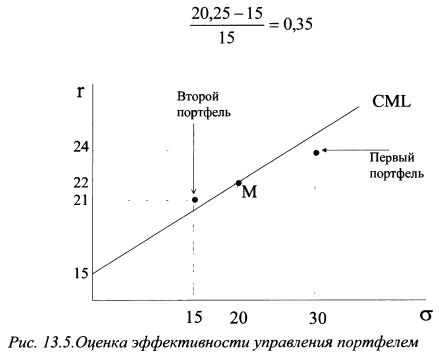
Для первого портфеля коэффициент Шарпа равен 0,3, в то время как для портфеля с аналогичным уровнем риска на С ML - 0,35. Поэтому можно сказать, что менеджер данного портфеля оказался не опытным в выборе конкретных активов, включил в портфель активы с большим нерыночным риском и не получил за него адекватного вознаграждения. Коэффициент Шарпа для второго портфеля равен 0,4, в то время как для портфеля на СML - 0,35. Это означает, что второй менеджер показал умение в выборе конкретных активов, т. е. включил в портфель активы с более высоким нерыночным риском, но и получил более высокую компенсацию. Результаты управления портфелями можно сравнить наглядно, как показано на рис. 13.5. Выше мы отметили, что, согласно коэффициенту Шарпа, первый менеджер оказался менее опытным в выборе активов чем второй. В то же время, при оценке деятельности по управлению портфелем не следует исключать и фактор возможной удачи. Чтобы судить более объективно о навыках управляющего, необходимо рассмотреть его результаты за относительно длительный период, как минимум несколько лет. Таким образом, сравнивая коэффициенты Трейнора и Шарпа, можно получить разные оценки управления портфелем относительно результатов рынка. Данное отличие возникает в связи с тем, что портфели могут содержать различную степень специфического риска даже при одинаковых значениях беты или иметь различную бету при одинаковых стандартных отклонениях.
|
||||||||||||
|
|
||||||||||||










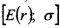 , коэффициент Шарпа представляет собой угловой коэффициент наклона линии, проходящей через ставку без риска и оцениваемый портфель, как показано на рис. 13.2.
, коэффициент Шарпа представляет собой угловой коэффициент наклона линии, проходящей через ставку без риска и оцениваемый портфель, как показано на рис. 13.2.

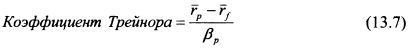
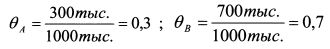
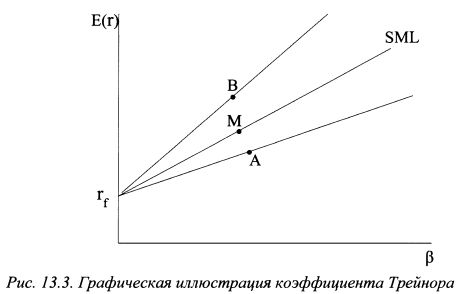
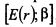 , коэффициент Трейнора представляет собой угловой коэффициент наклона линии, проходящей через ставку без риска и оцениваемый портфель, как показано на рис, 13.3. На рисунке представлена иллюстрация коэффициентов Трейнора для портфелей А и В. По сравнению с рыночным портфелем, расположенном на SML, портфель В управлялся более эффективно, а портфель А менее эффективно.
, коэффициент Трейнора представляет собой угловой коэффициент наклона линии, проходящей через ставку без риска и оцениваемый портфель, как показано на рис, 13.3. На рисунке представлена иллюстрация коэффициентов Трейнора для портфелей А и В. По сравнению с рыночным портфелем, расположенном на SML, портфель В управлялся более эффективно, а портфель А менее эффективно.


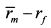 . Если коэффициент Трейнора портфеля больше
. Если коэффициент Трейнора портфеля больше 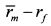 , то менеджер получил более высокое вознаграждение за риск по сравнению с требованием рынка в рамках пассивной стратегии. Если же коэффициент оказался меньше
, то менеджер получил более высокое вознаграждение за риск по сравнению с требованием рынка в рамках пассивной стратегии. Если же коэффициент оказался меньше 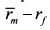 , то менеджер показал результаты хуже рынка.
, то менеджер показал результаты хуже рынка.