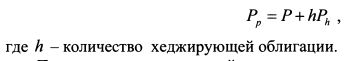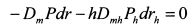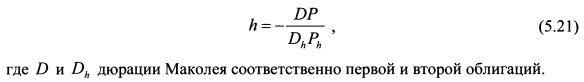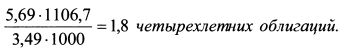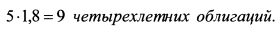5.1.2.3. Хеджирование портфеля облигаций с помощью показателя дюрации

При активном управлении портфелем облигаций может возникать необходимость страховаться от изменения стоимости портфеля при изменении процентной ставки на короткие периоды времени. Это можно сделать на основе дюрации портфеля. Рассмотрим технику хеджирования портфеля из одной облигации.

Инвестор владеет облигацией и хотел бы застраховаться от изменения ее стоимости. Цена облигации равна P, доходность до погашения - r, модифицированная дюрация – D_m. Облигация страхуется с помощью другой облигации, назовем ее хеджирующей облигацией. Цена ее равна P_h, доходность до погашения – r_h, модифицированная дюрация – D_mh. Для страхования стоимости позиции необходимо создать хеджирующий портфель, включив в него хеджируемую и хеджирующую облигации. Стоимость хеджирующего портфеля P_p равна:

При изменении процентной ставки стоимость портфеля изменится на величину dP_p:

Инвестор заинтересован в сохранении неизменной стоимости портфеля. Поэтому необходимо построить его таким образом, чтобы:

Изменение стоимости первой и второй облигаций можно представить как:

и

Подставим выражения для dP и dP_h в (5.15):

Найдем из равенства (5.18) величину h:

Выражение (5.19) определяет количество хеджирующей облигации в портфеле инвестора. Знак минус говорит о том, что вторую облигацию необходимо продать.

В случае параллельности сдвигов кривых доходностей при изменении процентных ставок dr = dr_h, и равенство (5.19) принимает вид:

В формулах (5.19) и (5.20) использована модифицированная дюрация. Если кривая доходности параллельна оси абсцисс, т.е. доходность до погашения для любых временных периодов одинаковая, то вместо модифицированной дюрации можно использовать дюрацию Маколея:

Пример.

Портфель инвестора состоит из пяти одинаковых облигаций, которые погашаются через восемь лет. Номинал облигаций 1000 руб., купон 12%, выплачивается один раз в год, цена 1106,7 руб. Портфель страхуется с помощью продажи четырехлетних облигаций. Их номинал 1000 руб., купон 10%, выплачивается раз в год, цена 1000 руб. Кривая доходности параллельна оси абсцисс. Дюрация Маколея четырехлетней облигации равна 3,49 года, восьмилетней - 5,69 года. Определить какое количество четырехлетних облигаций следует продать инвестору.

Решение.

В соответствии с формулой (5.21) на каждую восьмилетнюю облигацию следует продать:

Для страхования портфеля надо продать:

Содержание

Далее