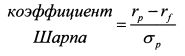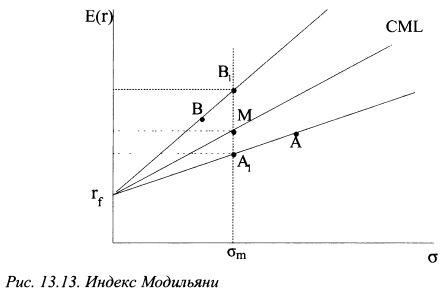
13.2.4. Индекс Модильяни

Индекс, который предложили Ф. и Л.Модильяни, сравнивает оцениваемые портфели не непосредственно, а через формирование на их основе соответствующих заемных или кредитных портфелей. Поясним данный способ вначале графически.

На рис. 13.13 представлены портфели А и В, результативность управления которыми необходимо сравнить, и рыночный портфель М. Риск рыночного портфеля равен ат. Вместо того, чтобы непосредственно сравнить портфели А и В, можно сравнить портфели Ai и /?/. Портфель Ai лежит на прямой, проходящей через ставку без риска и портфель А. Портфель Bj лежит на прямой, проходящей через ставку без риска и портфель В. Данные портфели располагаются на пересечении отмеченных прямых с линией, проходящей через рыночный портфель М и точку ат. Таким образом, портфель Ai представляет собой кредитный портфель относительно портфеля А. Портфель Bj является заемным портфелем относительно портфеля В. Поскольку портфели А], М и В] характеризуются одинаковым риском, то их можно сравнивать непосредственно. Результаты данного сравнения можно перенести уже на первоначальные портфели А и В.

Проведем рассуждения для определения индекса Модильяни в общей форме. Риск нового портфеля, построенного на основе оцениваемого портфеля, равен риску рыночного портфеля и составляет величину:

Из формулы (13.16) получаем:

Доходность портфеля n равна:

Таким образом, индекс Модильяни определяет премию за риск для портфеля, созданного на основе оцениваемого портфеля, риск которого равен риску рыночного портфеля. С помощью данного индекса можно оценивать результативность управления разными портфелями. Поскольку сравниваются созданные портфели с одинаковым риском (риск каждого равен ат), то лучшим результатом характеризуется портфель с наибольшим значением Мр, поскольку оно показывает величину премии за риск.

Следует, однако, отметить, что индекс Модильяни по своей сути есть не что иное как несколько модифицированная форма индекса Шарпа. Запишем индекс Модильяни, раскрыв в нем величину ер:

В выражении (13.20) величина ат является константой, так как это риск рыночного портфеля. Поэтому, с точки зрения сравнительной оценки портфелей ее можно исключить из формулы (13.20). В результате получаем коэффициент Шарпа:

Содержание

Далее