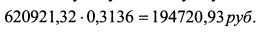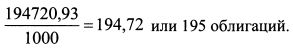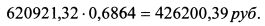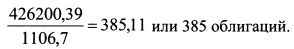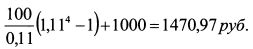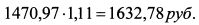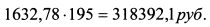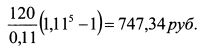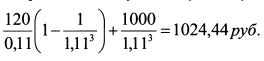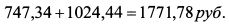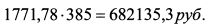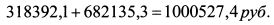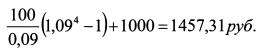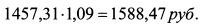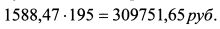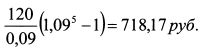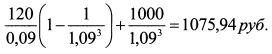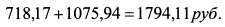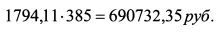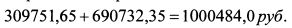|
||||||||||||
|
||||||||||||
| Какой брокер лучше? Альпари Just2Trade R Trader Intrade.bar Сделайте свой выбор! | ||||||||||||
| Какой брокер лучше? Just2Trade Альпари R Trader | ||||||||||||
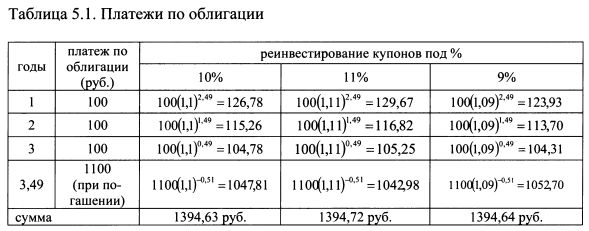
5.1.1.4. Иммунизация портфеля облигацийОдним из приемов пассивного управления портфелем является его иммунизация. Главный риск в отношении облигаций состоит в возможности изменения процентной ставки и, соответственно, цены облигации. Если менеджер стремится застраховаться от изменения стоимости портфеля облигаций к определенному моменту времени, то он должен сформировать его таким образом, чтобы дюрация портфеля соответствовала требуемому периоду времени. Тогда в случае изменения процентной ставки потери (выигрыши) в стоимости облигаций будут компенсироваться выигрышами (потерями) от реинвестирования купонов. Рассмотрим технику иммунизации вначале на примере портфеля, в который входит одна облигация. Пример 1. Номинал облигации 1000 руб., купон 10%, выплачивается один раз в год, время до погашения четыре года. Процентная ставка одинакова для всех периодов времени и равна 10% годовых, т.е. кривая доходности параллельна оси абсцисс на графике кривой доходности. Предполагается, что в случае изменения процентных ставок в течение времени обращения облигации кривая доходности будет смещаться параллельно. Купоны, получаемые по облигации, реинвестируются под текущий процент. Дюрация Маколея облигации равна 3,49 года. Это означает, что, если инвестор купит облигацию по текущей цене и продаст через 3,49 года, то он обеспечит по инвестициям в облигацию доходность 10% годовых, независимо от того, как будут изменяться процентные ставки на рынке. Данный факт проиллюстрирован расчетами, приведенными в таблице 5.1. В таблице приведены три варианта конъюнктуры на рынке. В третьей колонке представлена ситуация, когда процентная ставка оставалась неизменной в течение всех последующих четырех лет. От реинвестирования купонов под данную ставку до момента продажи облигации через 3,49 года и продажи облигации в это время инвестор в сумме получил 1394,63 руб. В четвертой колонке показано, что за первый год обращения облигации процентная ставка выросла на 1 % и оставалась неизменной в течение следующих трех лет. Поэтому все расчеты сделаны на основе 11%. В сумме инвестор получил 1394,72 руб. В пятой колонке конъюнктура соответствует случаю, когда в течение первого года ставка упала на 1% и оставалась неизменной на протяжении оставшегося времени. В итоге инвестор получил 1394,64 руб.
Таким образом, на момент времени равный дюрации облигации инвестор обеспечивает себе сумму денег порядка 1395 руб. независимо от изменения процентных ставок на рынке в течение обращения облигации. Данная сумма денег соответствует доходности в 10% годовых, так как инвестор купил облигацию за 1000 руб. и получил через 3,49 года 1394,6 руб.: Почему в примере в конце периода равного дюрации облигации инвестор обеспечивает себе одинаковую сумму денег независимо от изменения процентных ставок? Купонной облигации с погашением через четыре года можно поставить в соответствие во времени некоторую бескупонную облигацию. По бескупонной облигации инвестор гарантированно получает в момент погашения ее номинал. Если найти такое временное соответствие между облигациями, то по купонной облигации в этот момент инвестор также должен гарантированно получить сумму, равную номиналу данной бескупонной облигации. В нашем примере таким эквивалентом четырехлетней облигации с купоном 10% выступает бескупонная облигация с номиналом 1394,6 руб., которая погашается через 3,49 года. Пример 2. Процентная ставка одинакова для всех периодов времени и равна 10% годовых. Компания хотела бы инвестировать 620921,32 руб. под данный процент, чтобы обеспечить через пять лет выплату по своим обязательствам в размере 1 млн. руб. Если инвестировать данную сумму средств в пятилетний бескупонные облигации, то через пять лет она дорастет до 1 млн. руб.:
Допустим, что на рынке отсутствуют такие облигации. Поэтому компания решает инвестировать средства в купонные облигации. Купоны выплачиваются один раз в год. Первая облигация только что выпущена, погашается через четыре года, номинал 1000 руб., купон 10%, дюрация Маколея 3,49 года. Вторая облигация имеет номинал 1000 руб., купон 12%, погашается через восемь лет. Ее цена равна 1106,7 руб., дюрация Маколея 5,69 года. Чтобы застраховаться от изменения процентных ставок в течение следующих пяти лет, инвестору следует построить портфель таким образом, чтобы его дюрация была равна пяти годам, т.е. времени погашения обязательства. Поэтому суммы, на которые следует купить первую и вторую облигации, можно определить из системы уравнений:
Решая систему, получим: Четырехлетнюю облигацию следует купить на сумму:
Ее цена составляет 1000 руб. Поэтому необходимо купить:
Восьмилетнюю облигацию покупаем на сумму:
в количестве:
Рассмотрим динамику стоимости портфеля при изменении процентной ставки на рынке. Пусть в течение первого года ставка выросла на 1%. По первой облигации купоны реинвестируются до момента ее погашения под 11%. За следующие четыре года полученная сумма от реинвестирования купонов и погашения номинала одной облигации равна:
За пятый год данная сумма также реинвестируется под 11%:
Общая сумма средств, полученная по четырехлетним облигациям, составит:
По восьмилетней облигации сумма средств от реинвестирования купонов за пять лет равна:
От продажи облигации через пять лет будет получена сумма:
Общая сумма денег по одной восьмилетней облигации равна:
По всем восьмилетним облигациям она составляет:
Стоимость портфеля через пять лет равна:
Таким образом, через пять лет инвестор будет располагать 1млн. руб. для погашения своих обязательств. Рассмотрим другую ситуацию. Пусть в течение первого года ставка понизилась на 1%. По первой облигации купоны реинвестируются до момента ее погашения под 9%. За следующие четыре года полученная сумма от реинвестирования купонов и погашения номинала одной облигации равна:
За пятый год данная сумма также реинвестируется под 9%:
Общая сумма средств, полученная по четырехлетним облигациям, составит:
По восьмилетней облигации сумма средств от реинвестирования купонов за пять лет равна:
От продажи облигации через пять лет будет получена сумма:
Общая сумма денег по одной восьмилетней облигации равна:
По всем восьмилетним облигациям она составляет:
Стоимость портфеля через пять лет равна:
Таким образом, и в случае понижения процентной ставки инвестор будет располагать 1 млн. руб. через пять лет. Портфель с требуемым значением дюрации можно построить из отдельных облигаций с разными величинами дюрации, так как дюрация портфеля является средневзвешенной дюрацией отдельных облигаций. В то же время, если в портфель включены облигации с дюрациями, существенно отличающимися друг от друга, возникает риск иммунизации, который состоит в том, что при изменении конъюнктуры рынка кривая доходности не будет смещаться параллельно. Иммунизация портфеля дает эффективный результат для небольших изменений в процентных ставках. Данная стратегия содержит в себе элементы активных действий, так как портфель необходимо пересматривать при существенных изменениях процентной ставки и по прошествии некоторого времени. В последнем случае уменьшение времени и сокращение периода дюрации могут не совпадать. Поэтому портфель следует время от времени пересматривать с учетом новых процентных ставок и инвестиционного горизонта.
|
||||||||||||
|
|
||||||||||||








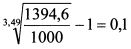 или 10%.
или 10%.
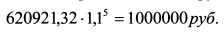

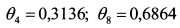 .
.